Attention Is All You Need: The Original Transformer Architecture

This newsletter is the latest chapter of the Big Book of Large Language Models. You can find the preview here, and the full chapter is available in this newsletter

• The Self-Attention Mechanism

• The Multi-head Attention Layer

• The Positional Encoding

• The Encoder

• The Residual Connections

• The Layer Normalization

• The Position-wise Feed-Forward Network

• The Decoder

• The Cross-Attention

• Masking The Self-Attention Layer

• The Prediction Head

• The Decoding Process

• Training For Causal Language Modeling

• Understanding the scale of the model

• Estimating The Number Of Model Parameters

• Estimating The Floating‐Point Operations

• The Different Architecture Variations

• The Encoder-Only Architecture

• The Decoder-Only Architecture

• The Encoder-Decoder Architecture

---

The "Attention Is All You Need" paper is one of the most influential works in modern AI. By replacing recurrence with self-attention mechanisms, the authors introduced the Transformer architecture, a design that enabled parallelized training, captured long-range dependencies in data, and scaled effortlessly to unprecedented model sizes. This innovation not only rendered RNNs obsolete but also laid the groundwork for BERT, GPT, and the modern LLM revolution, powering breakthroughs from conversational AI to protein folding. Beyond technical innovations, the paper catalyzed a paradigm shift toward general-purpose models with the rise of foundation models trained on massive datasets and reshaped industries from healthcare to creative arts. In essence, it transformed how humanity interacts with language, knowledge, and intelligence itself.

Architecture Overview

The original Transformer architecture is composed of the encoder that computes a rich representation of the input sequence, the decoder that generates the output sequence, and the prediction head that uses the decoder output to predict the tokens of the output sequence.

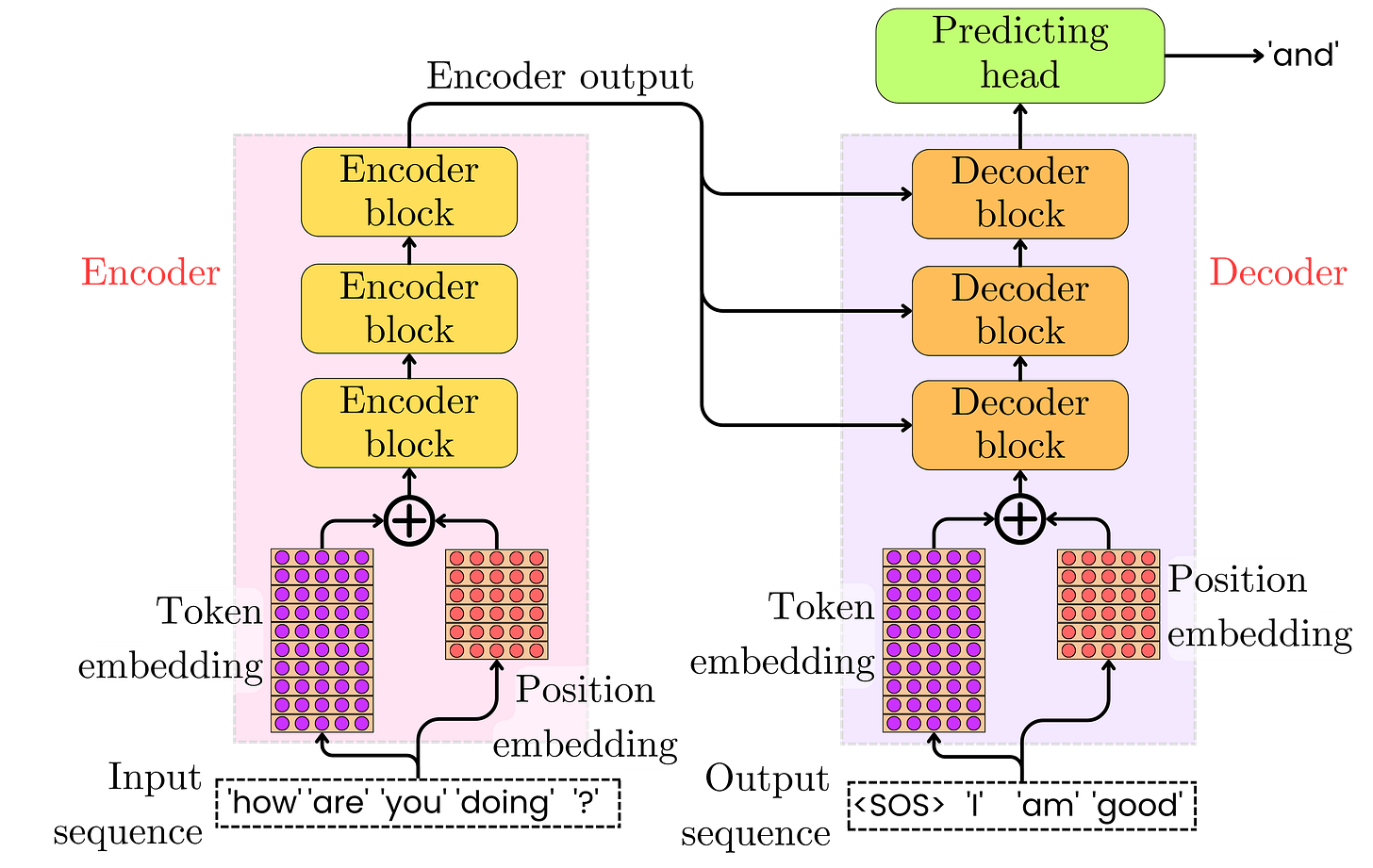
The architecture presented in the "Attention Is All You Need" paper builds directly from the RNN encoder-decoder architecture while discarding recurrence entirely and replacing Bahdanau/Luong's cross-attention with intra-sequence attention. There are four important components to the architecture:

• The embeddings: Besides the token embeddings necessary to project the tokens into their vector representations, the Transformer introduced the need for positional encoding to ensure that the information related to the token positions is captured by the model.

• The encoder: As for the RNN encoder-decoder, the encoder is in charge of encoding the input sequence into vector representations such that the decoder has enough information to decode the output sequence. It comprises a stack of identical encoder blocks, each with multi-head self-attention (capturing global dependencies) and a position-wise feed-forward network (applying non-linear transformations).

• The decoder: Similar to the encoder but adds masked multi-head self-attention (preventing future token visibility) and encoder-decoder attention (aligning decoder inputs with encoder outputs, akin to Bahdanau/Luong but without RNNs). As before, the autoregressive generation proceeds token-by-token.

• Prediction head: The prediction head is a classifier over the whole token vocabulary made out of a linear layer followed by Softmax, converting the decoder's final hidden states into token probabilities to predict the next word.

We will cover each component in detail in the remainder of this chapter. Self-attention and position embedding are central to the transformer architecture, and we need to discuss those technical innovations before we can understand the entire architecture.

The Self-Attention

The Self-Attention Mechanism

The Architecture

In the case of the Bahdanau/Luong attention, the goal was to capture the interactions between the tokens of the input sequence and the ones of the output sequence. In the Transformer, the self-attention captures the token interactions within the sequences. It is composed of three linear layers: W^K, W^Q, and W^V. The input vectors to the attention layer are the internal hidden states h_i resulting from the model inputs. There are as many hidden states as tokens in the input sequence, and h_i corresponds to the i^th token. W^K, W^Q and W^V project the incoming hidden states into the so-called keys k_i, queries q_i and values v_i:

\(\begin{align} \mathbf{k}_i &= W^K\mathbf{h}_i, \quad \text{keys} \nonumber\\ \mathbf{q}_i &= W^Q\mathbf{h}_i, \quad \text{queries} \nonumber\\ \mathbf{v}_i &= W^V\mathbf{h}_i, \quad \text{values} \end{align}\)

W^K, W^Q, and W^V are used to project the hidden states into keys, queries, and values.

The keys and queries are used to compute the alignment scores.

The keys and queries are used to compute the alignment scores:

\(e_{ij} = \frac{\mathbf{k}_i^\top\mathbf{q}_j}{\sqrt{d_{\text{model}}}}\)

As in the case of the Bahdanau attention, e_ij is the alignment score between the i^th word and the j^th word in the input sequence. d_model is the common naming convention for the hidden size:

\(\left\vert\mathbf{h}_i\right\vert=\left\vert\mathbf{k}_i\right\vert=\left\vert\mathbf{q}_i\right\vert=\left\vert\mathbf{v}_i\right\vert=d_{\text{model}}=\text{Hidden size}\)

The scaling factor √d_model in the scaled dot-product is used to counteract the effect of the dot product's magnitude growing with the dimensionality d_model, which stabilizes gradients and ensures numerical stability during training. It is common to represent to represent those operations as matrix multiplications. With the matrix K =[k₁, …, k_N] and Q =[q₁, …, q_N], we have:

\( E = \frac{Q^\top K}{\sqrt{d_{\text{model}}}}\)

or:

\( E = \frac{1}{\sqrt{d_{\text{model}}}} \begin{bmatrix} \mathbf{q}_1^\top \mathbf{k}_1 & \mathbf{q}_1^\top \mathbf{k}_2 & \cdots & \mathbf{q}_1^\top \mathbf{k}_N \\ \mathbf{q}_2^\top \mathbf{k}_1 & \mathbf{q}_2^\top \mathbf{k}_2 & \cdots & \mathbf{q}_2^\top \mathbf{k}_N \\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{q}_N^\top \mathbf{k}_1 & \mathbf{q}_N^\top \mathbf{k}_2 & \cdots & \mathbf{q}_N^\top \mathbf{k}_N \\ \end{bmatrix}\)

with N being the number of tokens in the sequence.

The attention weights are the result of normalizing the alignment scores by using the softmax transformation.

As for the other attentions, the alignment scores are normalized to 1 through a Softmax transformation:

\( a_{ij} = \text{Softmax}(e_{ij})=\frac{\exp(e_{ij})}{\sum_{j=1}^N \exp(e_{ij})}\)

where a_ij is the attention weight between the tokens i and j, quantifying how strongly the model should attend to token j when processing token i. Because we have Σ a_ij = 1, a_ij can be interpreted as the probability that token j is relevant to token i.

Each context vector is the result of a weighted average of the value vectors by using the attention weights.

The attention weights are used to compute a weighted average of the values vectors:

\( \mathbf{c}_i = \sum_{j=1}^N a_{ij}\mathbf{v}_j\)

In the jargon used in the previous chapter, c_i are the context vectors coming out of the attention layer, but we can think of them as another intermediary set of hidden states within the network. Using the more common matrix notation, we have:

\( C = AV^\top\)

where V =[v₁, …, v_N], C =[c₁, …, c_N] and A = Softmax(E) is the matrix of attention weights.

The entire attention layer process.

The whole set of computations happening in the attention layer can be summarized as the following equation:

\( C = \text{Softmax}\left(\frac{QK^\top}{\sqrt{d_{\text{model}}}}\right)V\)

The Keys, Queries, and Values Naming Convention

The names "queries," "keys," and "values" are inspired by information retrieval systems (such as databases or search engines). Each token generates a query, key, and value to "retrieve" relevant context from other tokens. The model learns to search for relationships between tokens dynamically.

The queries represent what the current token is "asking for." For example, the word "it" in "The cat sat because it was tired," the query seeks antecedents (e.g., "cat"). The keys represent what other tokens "offer" as context. In our example, the key for "cat" signals it is a candidate antecedent for "it." The values are the actual content to aggregate based on attention weights. The value for "cat" encodes its contextual meaning (e.g., entity type, role in the sentence, ...). For each query (current token), the model "retrieves" values (context) by comparing the query to all keys (other tokens). For example, let us consider the sentence:

"The bank is steep, so it's dangerous to stand near it."

• Query ("it"): "What does 'it' refer to?"

• Keys ("bank," "steep," "dangerous"): Highlight candidates for reference.

• Values: Encode the meaning of each candidate.

The model computes high attention weights between the query ("it") and keys ("bank," "steep"), then aggregates their values to infer "it" refers to the riverbank.

The Multi-head Attention Layer

The Naive Description

We have talked about self-attention so far, but we use the so-called multi-head attention layer in the transformer architecture. The multi-head attention layer works as multiple parallel attention mechanisms. By having multiple attention layers in parallel, they will be able to learn various interaction patterns between the different tokens in the input sequence. Combining those will lead to more heterogeneous learning, and we will be able to learn richer information from the input sequence. Think about the multi-head attention layer as an ensemble of self-attentions, a bit like the random forest is an ensemble of decision tree models.

We call "heads" the parallel attention mechanisms. To ensure that the time complexity of the computations remains independent of the number of attention heads, we need to reduce the size of the internal vectors within the layers. The hidden size dimensionality per head is divided by the number of heads:

\( d_{\text{head}} = \frac{d_{\text{model}}}{n_{\text{head}}}\)

where n_head is the number of heads. This implies that the hidden size has to be chosen so that it is divisible by the number of heads.

Each attention generates vectors of size d_head = d_model / n_head, depending of the number of heads.

Let us call H =[h₁, …, h_N] the incoming hidden states. Each head h generates resulting hidden states H’_h of size d_head = d_model / n_head:

\(H'_h = \text{Attention}_h(H)\)

To combine those heads' hidden states, we concatenate them, and we pass them through a final linear layer W^O to mix the signals coming from the different heads:

\( H' = \text{Concat}(H'_1, \ldots, H'_{n_{\text{head}}})W^O\)

The result of each head is concatenated, and the signals are further mixed by a final linear layer W^O.

To generate smaller hidden states, we need to reduce the dimensionality of the internal matrices. In each head, the projection matrices W^K, W^Q, and W^V take vectors of size d_model and generate vectors of size d_model / n_head.

To generate smaller context vectors, we underlying projection matrices W^K, W^Q, and W^V need to be of size d_model X d_head for each head.

The Tensor Representation

In reality, the projection matrices are not spread across multiple heads, but different sections of the matrices handle the projections for the different heads.

Although the information we have described so far about the multi-head attention layer is accurate, there is a critical subtlety to understand when it comes to its implementation. To illustrate the mathematical properties of the attention heads, we pictured separate "boxes" where each attention mechanism evolved in parallel, but in reality, they are slightly more connected. To fully utilize the efficient parallelization capability of the GPU hardware, it is critical to rethink every operation as a tensor operation. We described W^K, W^Q, and W^V of each head as separate matrices, but in practice, it is just three matrices that we conceptually break down by the number of heads needed.

Similarly, there is only one set of keys, queries, and values, and each head processes the entire sequence of tokens but operates on a distinct subset of features. The keys, queries, and values have dimension d_model X N, where N is the number of tokens in the input sequence. To specify each head's sub-segment explicitly, we reshape the matrices into 3-dimensional tensors with dimension n_head X d_head X N. Let us consider the incoming set of the hidden states. It is first projected into keys, queries, and values:

\(\begin{align} K = W^K H, \quad \text{shape: } d_\text{model}\times N\\ Q = W^Q H, \quad \text{shape: } d_\text{model}\times N \\ V = W^V H, \quad \text{shape: } d_\text{model}\times N \end{align}\)

We then reshape the resulting matrices into 3-dimensional tensors:

\(\begin{align} K' = \text{Reshape}(K), \quad \text{shape: } n_\text{head}\times d_\text{head}\times N\\ Q' = \text{Reshape}(Q), \quad \text{shape: } n_\text{head}\times d_\text{head}\times N \\ V' = \text{Reshape}(V), \quad \text{shape: } n_\text{head}\times d_\text{head}\times N \end{align}\)

The keys, queries, and values are reshaped into 3-dimensional tensors with dimension n_head X d_head X N, where each slice of the tensors corresponds to one head.

Reshaping is computationally efficient as it only reorganizes the tensor dimensions. When we compute the alignment scores E' from new tensors, this leads to N X N score for each head:

\(E' = \frac{Q' K'^\top}{\sqrt{d_{\text{head}}}}, \quad \text{shape: } n_\text{head}\times N\times N\)

Here, we use the shorthand notation K’^T to streamline the notation and imply permutation on the last two indices of the tensor, similar to the transpose operation for matrices:

\( k'_{ikj} = k_{ijk}'^\top , \quad \text{shape: } n_\text{head}\times N\times d_\text{head}\)

where k’_ijk is an element of K'. Notice that the way the operations are performed ensures the computation of N X N attention weights per head while keeping the number of arithmetic operations constant compared to the vanilla attention layer. The attention weights A' are obtained by normalizing on the last dimension:

\(a'_{ijk} = \text{Softmax}(e'_{ijk})=\frac{\exp(e'_{ijk})}{\sum_{m=1}^N \exp(e'_{ijm})}, \quad \text{shape: } n_\text{head}\times N\times N\)

again, e’_ijk is an element of the tensor E' and a’_ijk of the tensor A'. The context vectors are computed as the weighted average of the values with the attention weights:

\(c'_{ijl} = \sum_{k=1}^N a'_{ijk}v'_{ilk}, \quad \text{shape: } n_\text{head}\times d_\text{head}\times N\)

or in tensor notation:

\( C' = A'V'^\top, \quad \text{shape: } n_\text{head}\times d_\text{head}\times N\)

At this point, we have N context vectors of size d_head per head. We can reshape this tensor such that we have N context vectors of size d_model = n_head d_head:

\(C = \text{Reshape}(C'), \quad \text{shape: } d_\text{model}\times N\)

We described this earlier as the concatenation of the different heads' context vectors. As a way to combine further the signal coming from the different heads, we pass the resulting context vectors through a final linear layer:

\(C_{\text{final}} = W^OC, \quad \text{shape: } d_\text{model}\times N\)

The computation of the attention and context vectors across multiple heads happens in parallel by making use of efficient tensor operations for GPU computing.

This approach lets the model process information more efficiently than sequential methods, making it better at understanding both nearby and far-apart relationships in the data.

The Positional Encoding

The Structure

The goal of the positional encoding (a.k.a. position embedding) in the Transformer architecture is to inject sequential order information into the model, enabling it to understand the position of tokens in a sequence. Since Transformers process all tokens in parallel (unlike sequential models like RNNs), they lack inherent awareness of token order. Position embeddings address this by encoding positional data. Without positional information, the Transformer would treat the input as a "bag of words," losing critical order-dependent structure.

In the "Attention is all you need" paper, the positional encoding is defined as another embedding matrix with the same embedding size as the token embedding. The number of rows in the position embedding defines the maximum number of tokens that the model can ingest within a sequence, also known as the context size. The positional information of the token is added to the model by summing the semantic vector representations of the tokens from the token embedding and their positional vector representations from the position embedding. This ensures that the self-attention weights carry the positional information such that the order of the tokens impacts the model inference.

The first set of hidden states is computed by summing the vector representations from the token embedding with the position encoding.

Without the position encoding, the model could not understand the order of the tokens in the sequence.

The position embedding (PE) is a static matrix of numbers. If i is the index position of the vectors in the embedding, and j is the index position of the elements in the vectors, the matrix elements are defined by the following formula:

\(\text{PE}(i, j) = \begin{cases} \sin\left(\frac{i}{1000^{j/d_\text{model}}}\right) & \text{if $j$ is even} ,\\ \cos\left(\frac{i}{1000^{(j-1)/d_\text{model}}}\right) & \text{if $j$ is odd}, \end{cases}.\)

where i ranges in [0, context size - 1] and j in [0, d_model - 1].

Capturing The Relative Token Positions

The motivation behind this choice of sinusoidal functional form for positional encodings is so the model can more easily learn attention weights reflecting each token's relative position. It stems from the trigonometric identities for sine and cosine functions:

\(\begin{align} \sin(x + y) &= \sin(x)\cos(y)+\cos(x)\sin(y) \nonumber\\ \cos(x + y) &= \cos(x)\cos(y)-\sin(x)\sin(y) \end{align}\)

Let us consider a fixed offset k, and we apply the trigonometric identities to the encoding formula:

\(\begin{align} \sin(\omega_j(i + k)) &= \sin(\omega_j i)\cos(\omega_j k)+\cos(\omega_j i)\sin(\omega_j k) \nonumber\\ \cos(\omega_j(i + k)) &= \cos(\omega_j i)\cos(\omega_j k)-\sin(\omega_j i)\sin(\omega_j k) \end{align}\)

where 𝛚_j = 1 / 1000^j/dmodel. In matrix notation, we have:

\(\begin{bmatrix} \sin(\omega_j (i + k)) \\ \cos(\omega_j (i + k)) \end{bmatrix} = \begin{bmatrix} \cos(\omega_j k) & \sin(\omega_j k) \\ -\sin(\omega_j k) & \cos(\omega_j k) \end{bmatrix} \begin{bmatrix} \sin(\omega_j i) \\ \cos(\omega_j i) \end{bmatrix}.\)

Let us define PE(i, j) as:

\(\begin{align} \mathbf{PE}(i, j)&= \begin{bmatrix} \text{PE}(i, j) \\ \text{PE}(i, j+1) \end{bmatrix} = \begin{bmatrix} \sin(\omega_j i) \\ \cos(\omega_j i) \end{bmatrix}, \text{and}\nonumber\\ \mathbf{PE}(i+k, j) &=\begin{bmatrix} \text{PE}(i+k, j) \\ \text{PE}(i+k, j+1) \end{bmatrix}= \begin{bmatrix} \sin(\omega_j (i + k)) \\ \cos(\omega_j (i + k)) \end{bmatrix} \end{align}\)

We obtain:

\( \mathbf{PE}(i, j+k) = R_i(k) \mathbf{PE}(i, j)\)

where:

\( R_j(k)=\begin{bmatrix} \cos(\omega_j k) & \sin(\omega_j k) \\ -\sin(\omega_j k) & \cos(\omega_j k) \end{bmatrix}\)

In linear algebra, R_j(k) is called the rotation matrix and is used to perform a rotation in Euclidean space. Effectively, it means that PE(i+k, j) is the rotation of PE(i, j) by an angle -𝛚_jk.

So far, we have shown that, for two tokens with relative distance k, each pair of elements (j, j+1) within their positional encodings are related to each other through a rotation with angle -𝛚_jk. Let us call PE(i) = [PE(i, 0), PE(i, 1), …, PE(i, d_model)]. We can relate PE(i) and PE(i+k) through the pairwise rotation matrix:

\(\mathbf{PE}(i+k) = R(k)\mathbf{PE}(i)\)

where

\( R(k) = \begin{bmatrix} R_0(k) & 0 & \cdots & 0 \\ 0 & R_2(k) & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & R_{d_\text{model}-2}(k) \\ \end{bmatrix}\)

Graphical representation of pairwise rotation of the different elements in the position encodings for two tokens separated by k tokens.

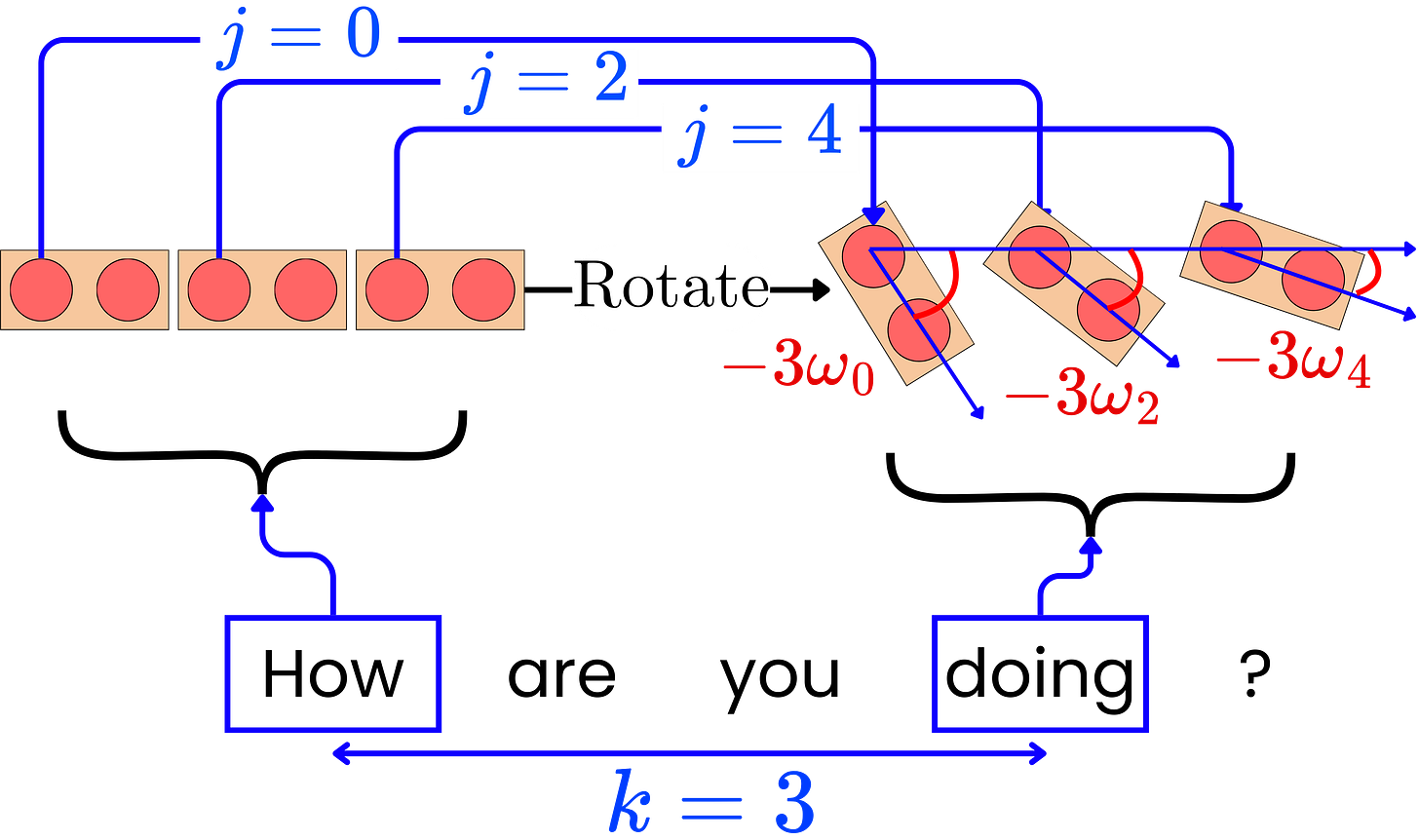
Let us now consider two hidden states h_i and h_i+k, corresponding to two tokens with relative distance k, coming into the self-attention layer. Both of them are the result of summing the token embedding vectors x_i and x_i+k and the positional encoding vectors PE(i) and PE(i+k):

\(\begin{align} \mathbf{h}_{i} = \mathbf{x}_{i} + \mathbf{PE}(i)\nonumber\\ \mathbf{h}_{i+k} = \mathbf{x}_{i+k} + \mathbf{PE}(i+k) \end{align}\)

We can compute their alignment score after projecting them into their keys and queries (we ignore heads for simplicity):

\(\begin{align} e_{i,i+k}&=\frac{\mathbf{q}_{i}^\top\mathbf{k}_{i+k}}{\sqrt{d_\text{model}}} \nonumber\\ &=\frac{\left(W^Q\mathbf{h}_{i}\right)^\top\left(W^K\mathbf{h}_{i+k}\right)}{\sqrt{d_\text{model}}}\nonumber\\ &=\frac{\left(W^Q\left[\mathbf{x}_{i} + \text{\textbf{PE}}(i)\right]\right)^\top\left(W^K\left[\mathbf{x}_{i+k} + \text{\textbf{PE}}(i+k)\right]\right)}{\sqrt{d_\text{model}}} \end{align}\)

When we compute the alignment score between two tokens separated by k tokens, we can decompose its value into various contributions, including how the relative position k interacts with the absolute position i.

If we expend, we obtain:

\(\begin{align} e_{i,i+k}\sqrt{d_\text{model}} &= \quad\underbrace{\mathbf{x}_i^\top W^{Q\top} W^K \mathbf{x}_{i+k}}_{{\text{Token-Token Interaction}}} \nonumber\\ &+\quad \underbrace{\mathbf{x}_i^\top W^{Q\top} W^K \mathbf{PE}(i) R(k)}_{{\text{Token-Position Interaction}}} \nonumber\\ &+ \quad\underbrace{\mathbf{PE}(i)^\top W^{Q\top} W^K \mathbf{x}_{i+k}}_{{\text{Position-Token Interaction}}}\nonumber\\ &+\quad \underbrace{\mathbf{PE}(i)^\top W^{Q\top} W^K \mathbf{PE}(i) R(k)}_{{\text{Position-Position Interaction}}} \end{align}\)

We effectively decomposed the alignment score into four components:

• Token-Token Interaction: Pure content-based alignment between x_i and x_i+k

• Token-Position Interaction: How the token at i interacts with the relative position k of x_i+k

• Position-Token Interaction: How the position i interacts with the token at x_i+k

• Position-Position Interaction: How the relative position k (encoded via R(k)) interacts with the absolute position i.

Let's remember that R(k) is the fixed, mathematically defined transformation matrix (from sinusoidal identities) that maps PE(i) to PE(i+k) and it exists purely as a property of the positional encoding scheme. With this linear relationship, the model parameters W^K and W^Q can learn to leverage the structure of positional encodings to compute attention scores that depend on content and relative positions. During training, the model will learn to weigh these interactions by adjusting W^K and W^Q. It makes the training more efficient as the model does not need to relearn positional relationships from scratch; it builds on the mathematical structure of PE(i). The sinusoidal nature of the encoding also helps the model to generalize better to both unseen absolute positions and positional offsets.

Positional Encoding's Multi-Frequency Design

The positional encoding defines a frequency that depends on the position of vector elements:

\(\omega_j=\frac{1}{10000^{j/d_\text{model}}}\)

Here, the constant 10,000 is a hyperparameter that controls the range of frequencies used to encode positional information. This means that the period of oscillations is 2𝝿 10000^j/dmodel. The frequencies range between [1, 1 / 10000^{(dmodel-1)/dmodel}]. High Frequencies lead to rapidly oscillating sine/cosine waves, which are adapted to distinguishing between nearby positions. This is crucial for local sentence syntax (e.g., word order in a phrase). Low frequencies lead to slowly oscillating waves that generalize over longer distances, which is useful for capturing global structure (e.g., paragraph-level coherence).

Each pair of columns captures different frequencies within the text data.

High Frequencies are adapted to distinguishing between nearby positions. This is crucial for local sentence syntax. Low frequencies are useful for capturing global structure.

The high value of 10,000 ensures a smooth transition from high to low frequencies across the embedding dimensions. 2𝝿 10000 is the maximum period supported by the model. Theoretically, this means it allows unique positional signals for tokens up to 2𝝿 10000 ~ 62,832 positions. However, transformers trained on sequences of fixed, shorter lengths (e.g., 512–4096 tokens) do not learn to handle positional relationships beyond this range. While the encoding theoretically supports very long periods, the model's effective context size is constrained by training data.

The Encoder