Deep Dive: Tuning XGBoost Hyperparameters with Bayesian Optimization

Deep Dive in Data Science Fundamentals

---

Hyperparameter Optimization can be a challenge for Machine Learning with large dataset and it is important to utilize fast optimization strategies that leads to better models. Bayesian optimization is a typical approach to automate hyperparameters finding. Today, we review the theory behind Bayesian optimization and we implement from scratch our own version of the algorithm. We use it to tune XGBoost hyperparameters as an example. Here is what we will cover:

• Bayesian Optimization algorithm and Tree Parzen Estimator

• Implementation: Tuning XGBoost

  • The search space

  • Creating data to learn from

  • Assessing a sample

  • Assessing the initial samples

  • Splitting the distribution

  • Sampling the “good” distribution

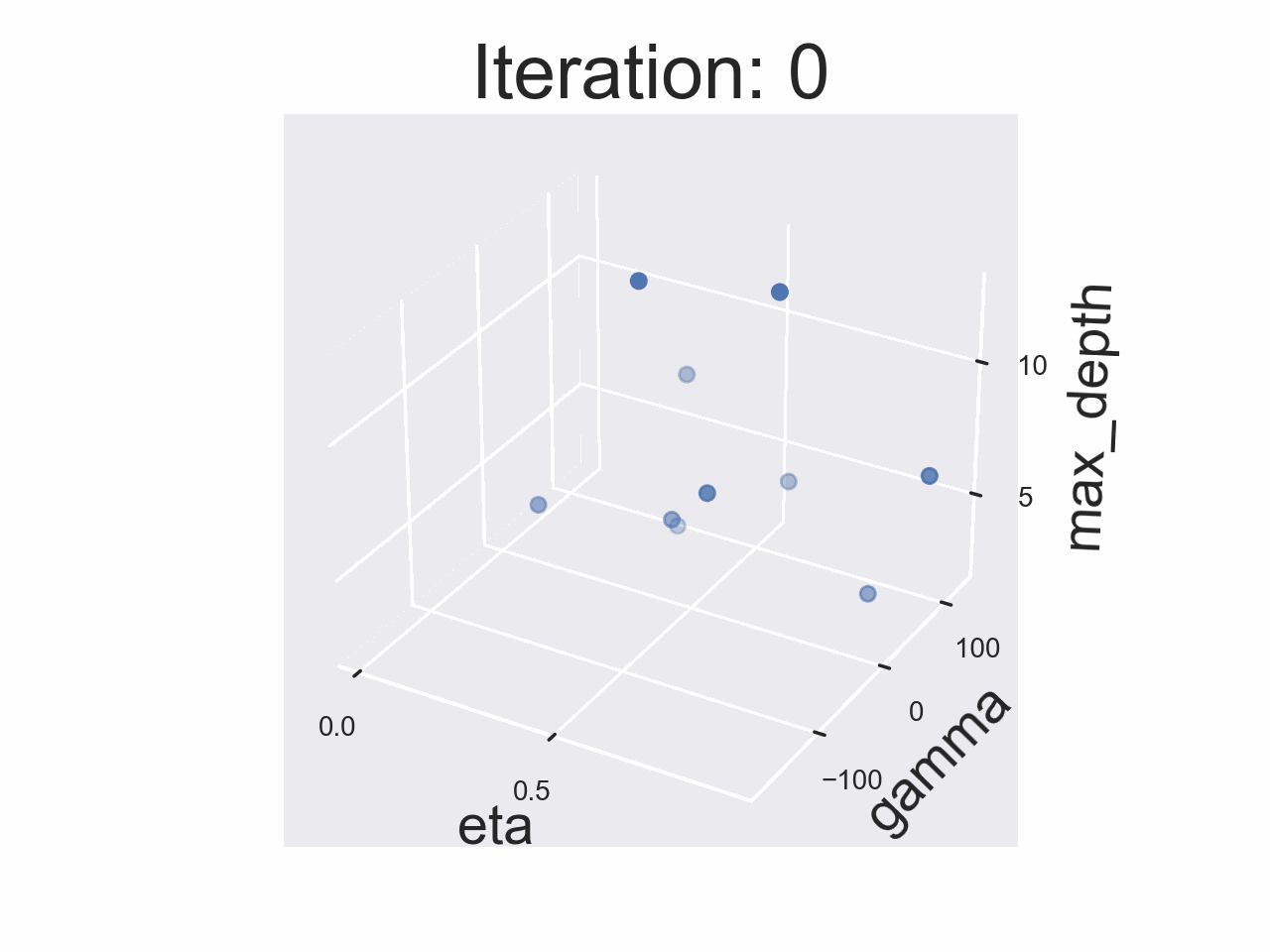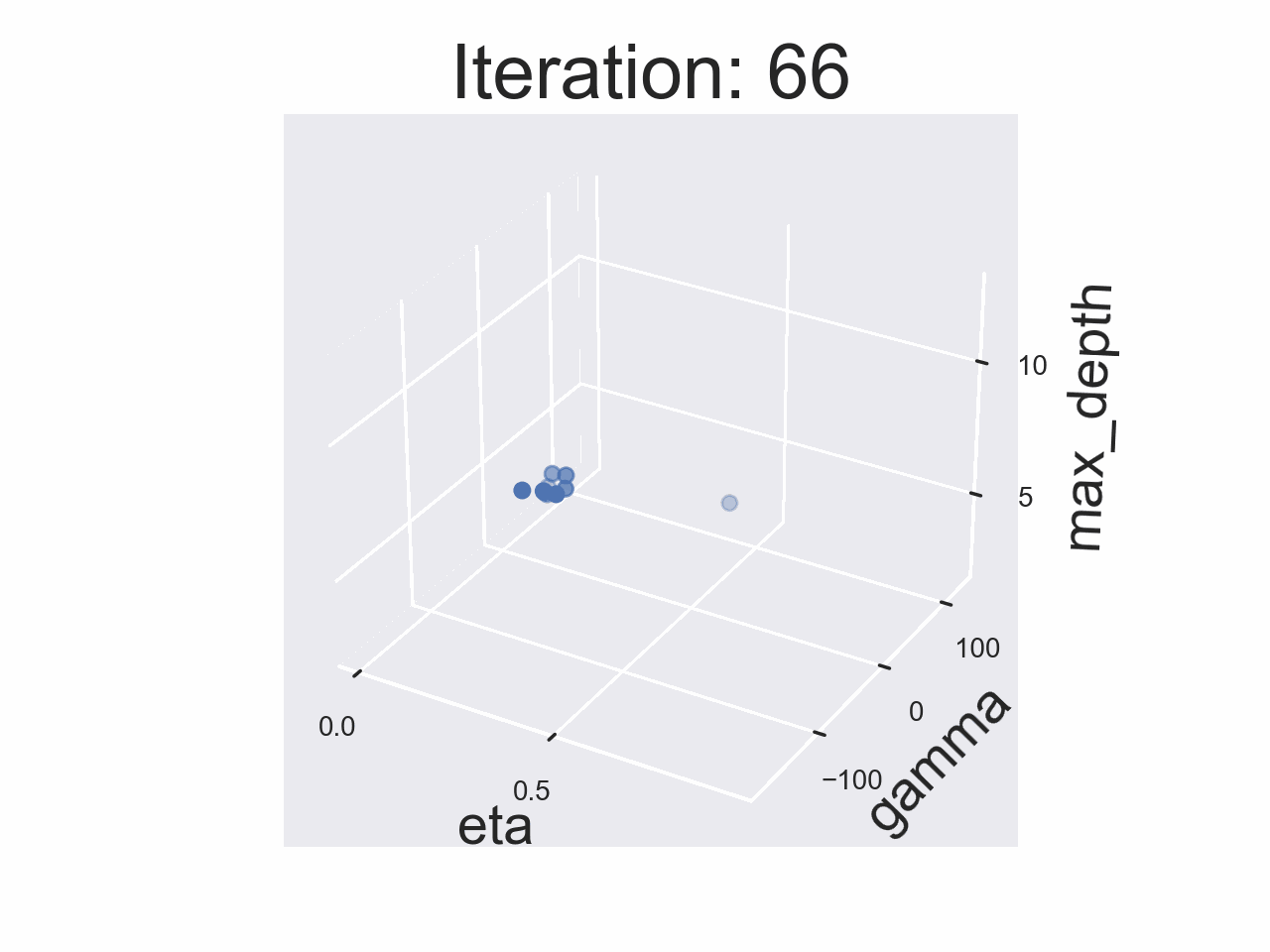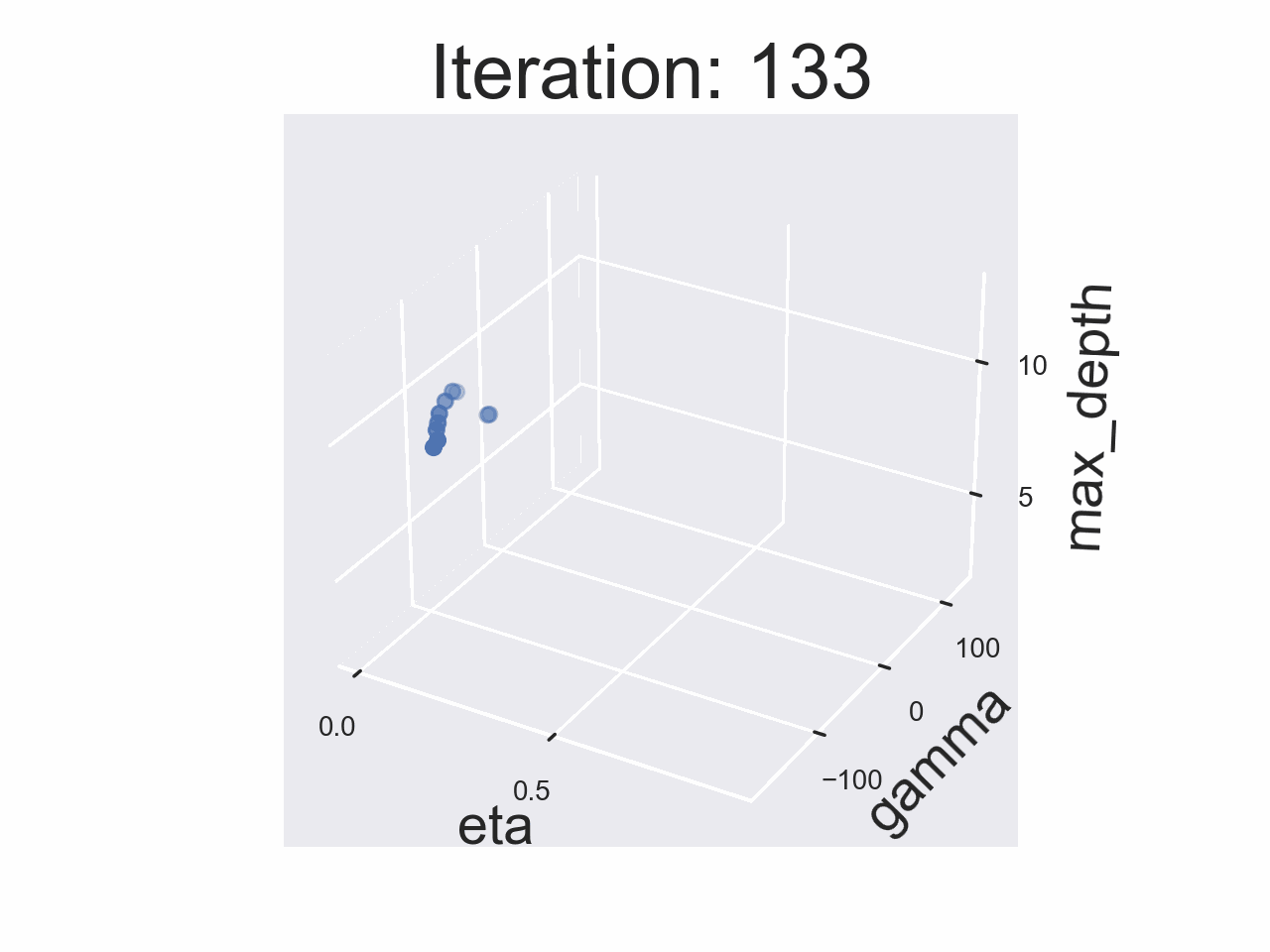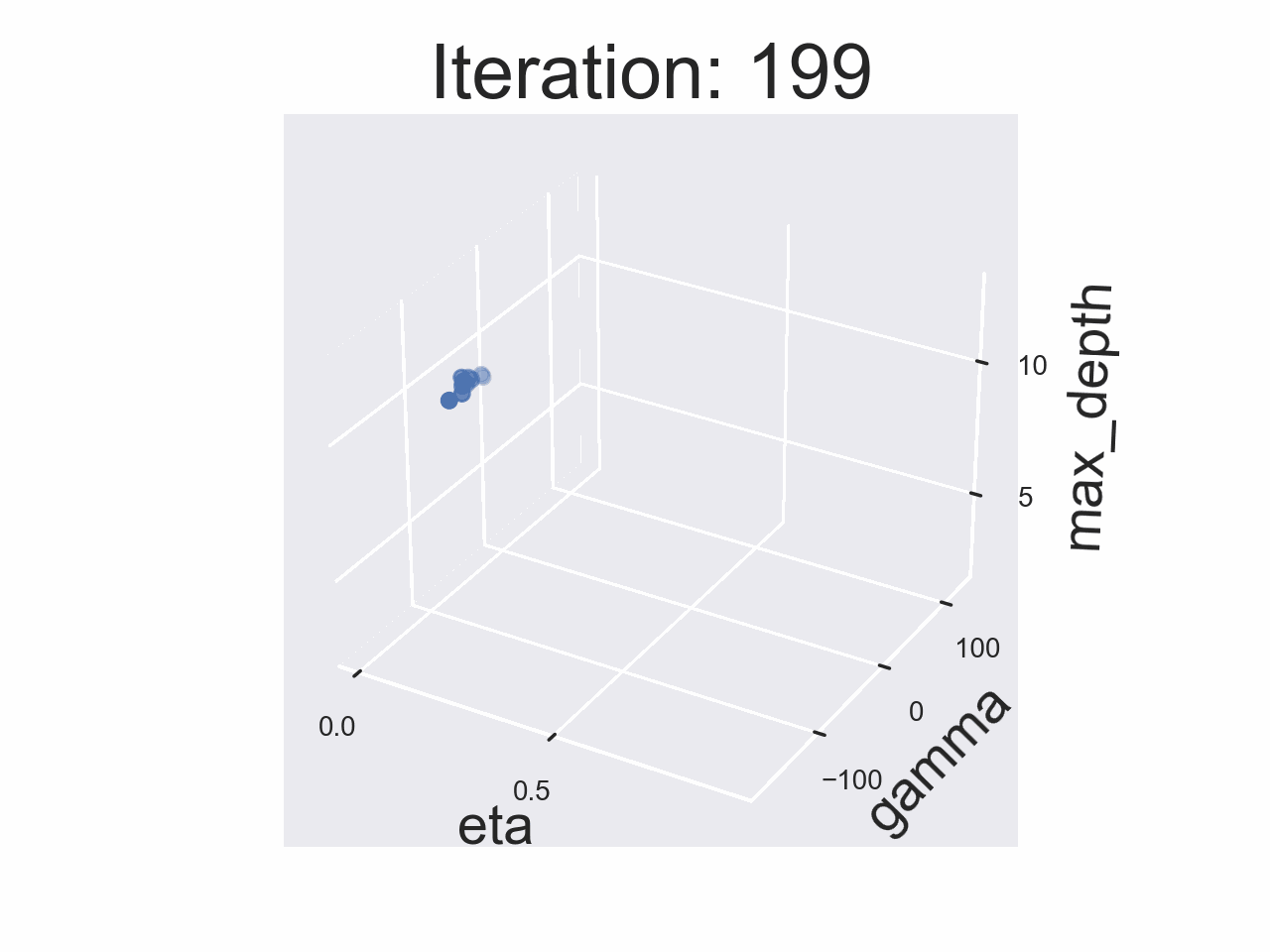
  • Running the whole experiment

  • The results

---

This Deep Dive is part of the Data Science Fundamentals series

Hyperparameter Optimization

For a specific learning task, one must consider the 4 following axes to find an optimal estimator:

• The model space: all the possible Machine Learning models that could be applied to the problem.

• The parameter space: all the parameter values a specific model could have. For a neural network for example, we refer to the weights of the model. For a tree-based model, we refer to all the possible splits trees could have.

• The feature space: all the possible subsets of the original features.

• The hyperparameter space: typically the hyperparameters refer to the model parameters that are not automatically learned by an optimization algorithm. In a neural network, the back-propagation algorithm allows us to learn the weights of the model but cannot tell us anything about the number of layers the model should have. The number of layers is a hyperparameter and one has to find additional optimization principle to find the best one.

For all those spaces, the idea is always the same: find the components (M: model, P: parameters, F: features, H: hyperparameters) that minimize the loss function L!

\(\{M, P,F, H\}^* = \arg\min_{M,P, F,H} L(M, P, F,H)\)

In the case M and F are fixed and P depends on the choice of H, the Hyperparameter Optimization problem is simply

\(H^* = \arg\min_H L(H)\)

Bayesian Optimization and the Tree Parzen Estimator

Let’s consider a set of d hyperparameters H = {h₁, …, h_d}. Each realization of H correspond to a performance metric L of the model on a validation data. If we try many hyperparameter values, we would get different performance metrics. The question is: what are the values of H that minimize L?

Let’s say we already measured some performance metrics for some hyperparameters

\(D=[(H_1,L_1), (H_2, L_2), \ldots, (H_m, L_m)]\)

Let’s find a threshold ⍺ being the 20th (for example) percentile of {L₁, L₂, …, L_m}. Using that threshold we could split the data into two sets

\(\begin{align} D_l &= D \text{ where } L < \alpha \\ D_g &= D \text{ where } L \geq \alpha \end{align} \)

D_l represents the set of “good“ hyperparameters since they have lower corresponding performance metrics L and D_g represents the set of “bad“ hyperparameters. If we estimate the distributions

\(\begin{align} l(H) &= p(L <\alpha | H, D) \\ g(H) &= p(L\geq \alpha | H, D) \\ \text{with } p(L|H,D) &= l(H) + g(H) \end{align}\)

If we were to sample L ~ p(L | H, D), we would want L to be as small as possible, so we want to maximize the probability distribution of the “good“ samples l(H) and minimize the probability distribution g(H) of the “bad“ ones. The algorithm is as follows:

• Choose some hyperparameters randomly and measure the resulting performance.

  

• Find a threshold ⍺ from that data and split the data into 2 sets D_l and D_g.

• Fit the kernel density distribution estimators for l(H) and g(H).

• Sample hyperparameters from the l(H) distribution and keep the one that maximizes l(H) / g(H). By maximizing l(H) / g(H) we both maximize l(H) and minimize g(H).

  

• With this new sample, recompute ⍺, l(H) and g(H) and iterate until convergence

  

Implementation: Tuning XGBoost

The search space

Let’s implement this algorithm in code! Let’s first understand how we capture the search space. Let’s consider the following hyperparameters for XGBoost:

=> eta, gamma, max_depth, min_child_weight, max_delta_step, subsample, lambda, alpha.

Look at the documentation for more information: XGBoost Parameters. Let’s define initial sampling distribution so that we can create initial samples to test.

from scipy import stats

search_space = {
    'eta': stats.uniform,
    'gamma': stats.expon(scale=50),
    'max_depth': stats.randint(low=1, high=15),
    'min_child_weight': stats.expon(scale=10),
    'max_delta_step': stats.expon(scale=10),
    'subsample': stats.uniform,
    'lambda': stats.expon(scale=5),
    'alpha': stats.expon(scale=5)   
}

We can now create a function that generates initial samples

import pandas as pd

def sample_priors(space, n_samples):

    # we are using a data frame to store the samples
    samples = pd.DataFrame(columns=space.keys())
    
    # we generate n_samples for each hyperparameter
    for key, dist in space.items():
        samples[key] = dist.rvs(size=n_samples)
    
    return samples

samples = sample_priors(search_space, 20)