How To Construct Self-Attention Mechanisms For Arbitrary Long Sequences

Toward Infinite Sequence Lengths

With Gemini models having a 2M tokens context size and Claude having a 200K tokens context size while having a time-to-first-token this fast, it is impossible not to have a modification of the attention mechanism that explicitly handles extremely long sequences. Considering the size of those models, 2M tokens would lead to Petabytes of GPU memory to generate each token! So, we need strategies to handle those sequence sizes efficiently! Let’s dive in:

• Transformer-XL

• Memorizing Transformers

• Infini-Attention

---

In the previous newsletters, we examined methods to reduce attention's computational complexity. In this newsletter, we are going to focus on designing attention mechanisms specifically optimized for processing extremely long contexts. The fundamental difference lies in the objective. Low-complexity attention methods primarily aim to approximate standard attention more efficiently, whereas long-sequence attention mechanisms fundamentally rethink how information flows across distant positions. Rather than merely making attention more computationally feasible, we are going to look at strategies to make distant contextual information meaningfully accessible and useful to the model.

Transformer-XL

Transformer-XL was proposed in 2019 as a way to process sequences of virtually unlimited length while maintaining coherent information flow across the entire document. The main limitations to handle sequences of any length are:

• The typical time complexity O(N²) of the attention layers. However, we have already seen strategies to reduce that complexity to O(N). For an autoregressive process, we are bounded from below by, at least, a linear decoding process in the sequence length. Therefore, we can never do better than this theoretical constraint.

• The absolute positional encoding proposed in the original "Attention is all you need" paper is the main blocker for encoding arbitrary sequence lengths. We would need a way to encode any possible positions, which is hard in practice.

• Another important blocker is the memory constraint. Longer sequences take more space in memory, and we would reach an upper bound in length when the GPU memory becomes saturated. We saw when discussing the FlashAttention that a high-end NVIDIA A100-8GB could realistically handle a maximum sequence length of 5,932 for a GPT-3 model.

With Transformer-XL, we are going to design an attention mechanism that processes sequences with linear time complexity, constant memory complexity, and a novel relative positional encoding that captures the relative distance between tokens instead of their absolute positions. We are going to delay diving into the relative positional encoding until a future newsletter and focus here on how to process arbitrary sequence lengths in linear time with bounded memory constraints.

To illustrate how it works, let's consider the following toy example of input sequence:

"Teaching computers to see the world makes every colorful dataset an adventure"

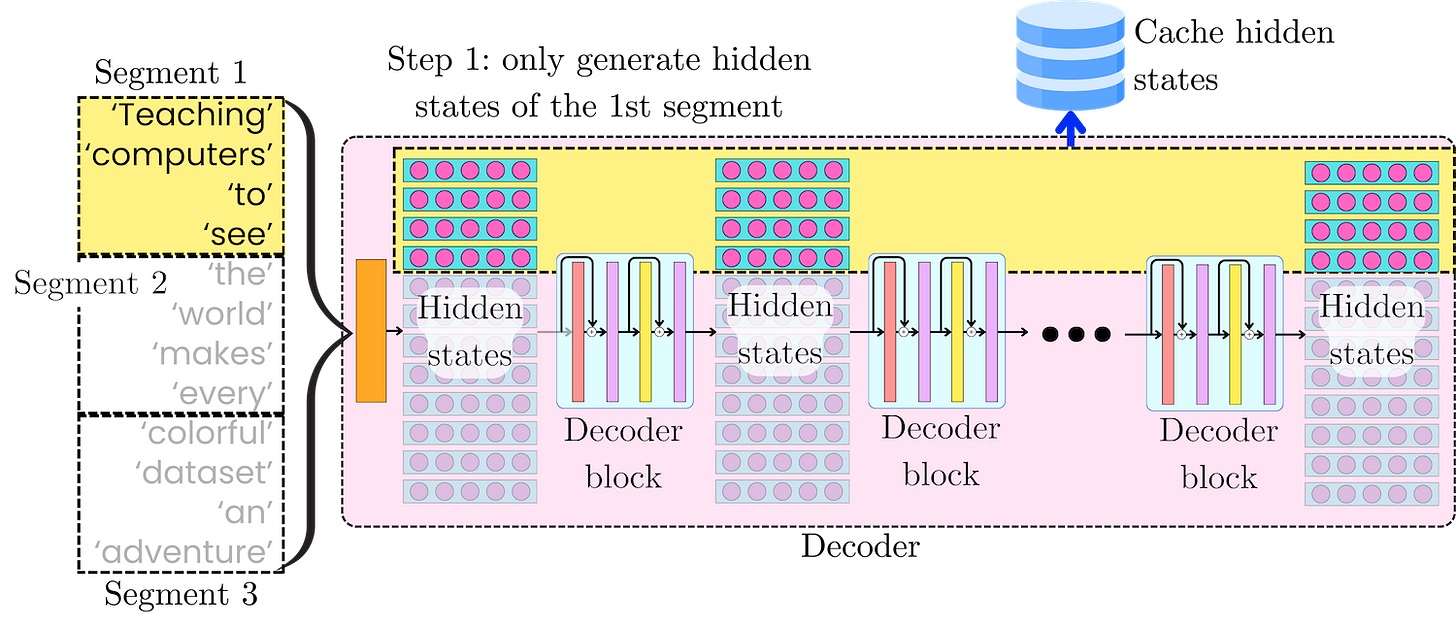
The strategy with Transformer-XL is to handle the incoming tokens by segments. We break down the incoming sequence into segments, typically of size ~128-512 tokens during training and up to 1600 tokens during evaluation. For our toy example, let's assume that our segments are four tokens long:

• Segment 1: ['Teaching', 'computers', 'to', 'see']

• Segment 2: ['the', 'world', 'makes', 'every']

• Segment 3: ['colorful', 'dataset', 'an', 'adventure']

Formally, we divide the incoming sequence into T = N / n segments, where n is the number of tokens per segment. We are going to create a segment-level recurrence to generate the output vectors from the model:

1. Generate all the hidden states [H¹₁, H²₁, …,H^L₁] related to the first segment 𝝉 = 1. l ∈ {1, …, L} is the index of the layer l, and L is the total number of layers in the model. The full attention is computed within segments, so its time and memory complexity is O(n²). We are going to cache the intermediate representations of the tokens [H¹₁, H²₁, …,H^L₁] for the next iteration.

   

2. In the next iteration, we are going to consider the second segment and its interaction with the first segment. At each layer, we retrieve the hidden states of segment 𝝉 = 1 and append them to the hidden state of segment 2

   \(\tilde{H}_2^l=\left[H_1^l;H_2^l\right]\)

   and we compute the next hidden states by passing them through the layer:

   \(H_2^{l+1}=\text{Layer}_l\left(\tilde{H}_2^l\right)\)

   Here, the attention matrix is computed across segments 1 and 2 and is, therefore, of size 2n x 2n, which still follows a quadratic complexity ~O(n²).

   

3. In general, for any segment 𝝉, we retrieve the computed hidden states [H¹_𝝉-1, H²_𝝉-1, …,H^L_𝝉-1] for the previous segment 𝝉 - 1, and append them to the hidden states of the current segment H^l_𝝉 for layer l:

   \(\tilde{H}_{\tau}^l=\left[H_{\tau-1}^l;H_{\tau}^l\right]\)

   and compute the next hidden states:

   \(H_{\tau}^{l+1}=\text{Layer}_l\left(\tilde{H}_{\tau}^l\right)\)

   At every point during this recurring process, the time and space complexity is at most ~O(n²), and we iterate this process until we reach the last segment in the sequence.

   

The recurrence mechanism effectively creates a form of "memory" that allows the model to maintain coherent understanding across very long texts while keeping computational requirements manageable. Transformer-XL's ability to maintain coherence across long contexts is directly related to its depth. H^l+1_𝝉 depends on H^l_𝝉-1 and H^l_𝝉, which means that the generation of the n hidden states in H^l+1_𝝉 depends on the 2 x n hidden states in [H^l_𝝉-1; H^l_𝝉]. The hidden states H^l_𝝉-1 also depend on H^l-1_𝝉-2 and H^l-1_𝝉-1. Therefore, H^l+1_𝝉 depends on the 3 x n hidden states in H^l_𝝉, H^l-1_𝝉-1, H^l-1_𝝉-2. If we go back k layers in the model, then the hidden states in H^l+1_𝝉 depend on the (k+1) x n hidden states in [H^l-k+1_𝝉, H^l-k+1_𝝉-1, …, H^l-k+1_𝝉-k]. By unrolling the recurrence of the hidden states' dependency, we establish the functional relationship:

\( H_{\tau}^{l+1}=f_k(H_{\tau}^{l-k+1}, H_{\tau-1}^{l-k+1}, \ldots, H_{\tau-k}^{l-k+1})\)

This creates a recurrence relation where information from segment 𝝉 −k can reach the final layer L in segment 𝝉 only if k+1 ≤ L. If we want to cover all the N tokens in the sequence, with k = N/n - 1, this means we need:

\(\begin{align} &\frac{N}{n} \leq L \nonumber\\ \text{or equivalently } &N \leq nL \end{align}\)

The theoretical dependency length is, therefore, O(n x L). If the network is not deep enough, its ability to propagate information across segments would be limited. This is because information flows through layers within a segment before being passed to the next segment. A shallow Transformer-XL would still have the unbounded context mechanism but might not effectively utilize information from distant parts of the sequence.

So far, we have only considered the forward pass, but it becomes messy when we consider the backward pass! When we compute the gradient of the loss function L, we need to compute its relation to the hidden states H^l+1_𝝉:

\(\begin{align} \frac{\partial \mathcal{L}}{\partial H_{\tau-k}^{l-k+1}}&=\sum_{i=l-k+1}^{l+1}\sum_{j=\tau-k}^\tau\frac{\partial \mathcal{L}}{\partial H_{j}^{i}}\cdot\frac{\partial H_{j}^{i}}{\partial H_{\tau-k}^{l-k+1}} \end{align}\)

The layer-wise summation

\(\sum_{i=l-k+1}^{l+1}\)

must consider all layers from l-k+1 up to l+1 and the segment-wise summation

\(\sum_{j=\tau-k}^\tau\)

must consider all segments from 𝝉 −k up to 𝝉. This creates (k+1)² gradient paths for a single hidden state segment. Now, for a sequence of length N divided into N/n segments, if we extend this to consider all possible hidden states that influence the loss, we get approximately:

\( \sum_{k=1}^{N/n}(k+1)^2\approx \frac{\left(N/n\right)^3}{3}\sim\mathcal{O}(N^3)\)

gradient paths to compute. This cubic growth makes training infeasible for long sequences. We are going to modify the segment-level dependency by introducing the Stop-Gradient SG(.) operator (detach in PyTorch):

\( \tilde{H}_{\tau}^l=\left[SG(H_{\tau-1}^l);H_{\tau}^l\right]\)

This operation prevents gradients from flowing backward through the cached states during backpropagation. This means:

\(\begin{align} SG(H_{\tau-1}^l) &= H_{\tau-1}^l\quad &\text{During the forward pass}& \nonumber\\ \frac{\partial \tilde{H}_{\tau}^l}{\partial SG(H_{\tau-1}^l)}&=0 \quad &\text{During the backward pass} \end{align}\)

By applying SG(.), the previous segment hidden states H^l_𝝉-1 is treated as constant during the backward pass. When we apply SG(.) to prevent gradient flow across segment boundaries, we introduce a profound asymmetry:

• Information Asymmetry: During the forward pass, the model can access and use information from previous segments, but during backpropagation, it cannot receive gradient signals from future segments.

• Truncated Credit Assignment: The model cannot directly attribute credit or blame to decisions made in previous segments, even though those decisions influence future outcomes.

This creates a unique learning paradigm where the model must learn to encode useful information in its hidden states without direct optimization signals for long-range dependencies. Interestingly, despite not being directly optimized for very long dependencies, Transformer-XL still develops impressive long-range capabilities because the recurrence mechanism creates paths for information to propagate forward.

For any two layers a and b, we have:

\( \frac{\partial H_{\tau'}^{a}}{\partial SG(H_{\tau}^{b})}=0 \quad\text{ if } \tau'\neq \tau\)

Therefore, the loss backpropagation simplifies to

\(\begin{align} \frac{\partial \mathcal{L}}{\partial H_{\tau-k}^{l-k+1}}&=\sum_{i=l-k+1}^{l+1}\frac{\partial \mathcal{L}}{\partial H_{j}^{i}}\cdot\frac{\partial H_{j}^{i}}{\partial H_{\tau-k}^{l-k+1}} \end{align}\)

which reduces the computational complexity from the cubic behavior O((N/n)³) to the linear one O(N/n) .

Each segment has length n, and when processing a single segment, attention is computed over the current segment plus the cached previous segment. The time complexity of the computation per segment is, therefore, ~O(4n²) = O(n²). For a sequence of length N, we process approximately T = N/n segments, and each segment requires O(n²). Therefore, the complexity of the total operations is:

\(\mathcal{O}\left(\frac{N}{n} \times n^2\right) = \mathcal{O}(N n)\)

Which is linear in the sequence size N. When it comes to the way the attention is computed, it is a very similar pattern to the sparse attention with a sliding window. Beyond the current and past segments, the hidden states are blind to the other tokens.

However, with sparse attention, the memory requirements grow linearly with the sequence size, but with Transformer-XL, the space complexity is bounded by O(n²) = O(1) as n is a fixed number. We still need to choose n large enough to make efficient use of the high GPU parallelism.

Memorizing Transformers

In Transformer-XL, the long-range coherence is captured by the successive layers in the model, but the direct interaction between tokens is lost beyond a two-segment window. Google introduced the Memorizing Transformers in 2022 that extended the long-range coherence by caching previous key-value pairs for selective retrieval. The attention computation is broken down into two parts:

• The local attention: As before, we partition the input sequence into segments (usually 512 tokens) and compute the token-token interactions within each segment:

  \( C_\text{local} = \text{Softmax}\left(\frac{Q_\text{local}K^\top_\text{local}}{\sqrt{d}}\right)V_\text{local}\)

  where Q_local, K_local, and V_local are the local queries, keys, and values within the segment.