How To Linearize The Attention Mechanism!

Today, we talk about how to engineer attention mechanisms in O(n) complexity instead of O(n²). This newsletter tends to be a bit more math-flavored than my usual content, but it is liberating to be able to use math for the greater good!

• Low-Rank Projection of Attention Matrices: Linformer

• Recurrent Attention Equivalence: The Linear Transformer

• Kernel Approximation: Performer

---

Self-attention’s quadratic complexity in sequence length has long been a central bottleneck for large-scale Transformer models. Handling tens of thousands of tokens becomes computationally prohibitive and can quickly exhaust available memory. Linear attention mechanisms represent a paradigm shift in transformer architecture by mathematically re-engineering the attention operation to achieve O(n) complexity while maintaining global context awareness. Unlike sparse attention's pattern restrictions, which preserve quadratic complexity but limit interactions to predefined token subsets, linear attention fundamentally redefines how all tokens interact by reformulating the attention matrix computation rather than pruning token interactions. Where sparse attention sacrifices theoretical completeness for practical speed, linear attention preserves global relationships at the cost of approximating pairwise token influences. This enables native handling of extreme sequence lengths (1M+ tokens) while avoiding sparse attention's blind spots.

Low-Rank Projection of Attention Matrices: Linformer

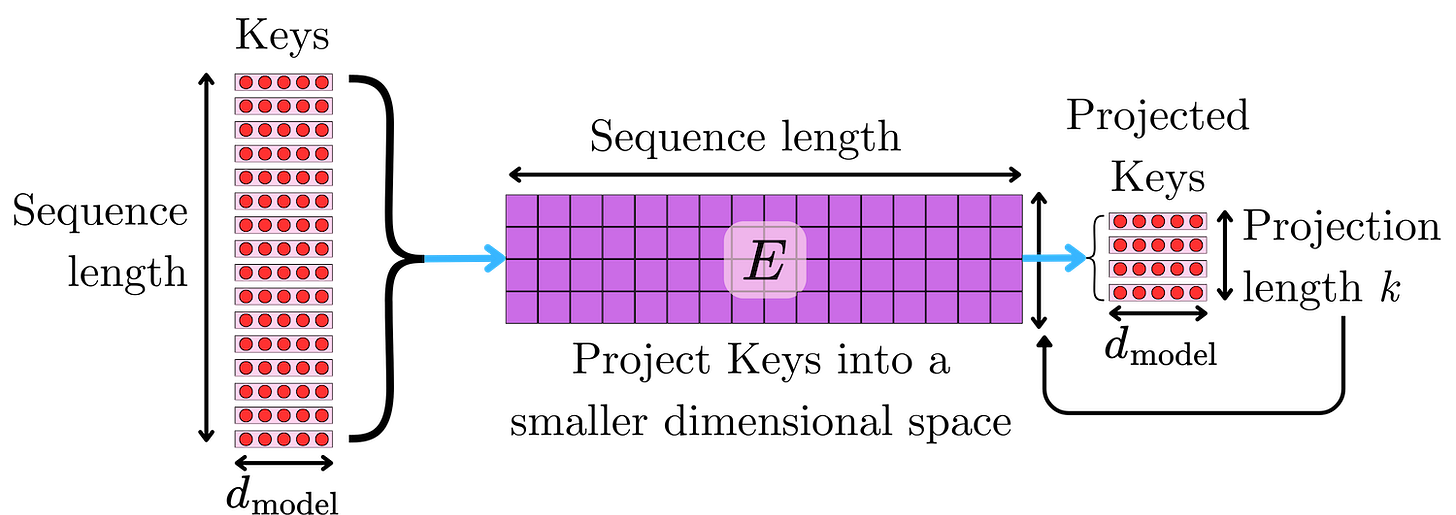
With Sparse attention mechanisms, we understood that most of the token interaction information was contained in a small subset of token pairs. Linformer introduced the idea that the token-token interaction matrix could be compressed into a smaller representation without too much information loss. Instead of computing the full N x N interaction Q^TK / √d (ignoring heads for simplicity), we could first project K into a lower rank dimension k, and compute the lower rank N x k approximation:

\( \frac{Q^\top EK}{\sqrt{d}}\)

where E is a N x k projection matrix that projects K from the original dimension d x N to d x k. This leads to N x k alignment score and attention matrices.

When we project with E, the approximation leads to the error:

\(\text{error} = \left\vert\frac{Q^\top K}{\sqrt{d}}-\frac{Q^\top EK}{\sqrt{d}} \right\vert\)

If the elements of E follow a Gaussian distribution ~N(0, 1/k), the Johnson–Lindenstrauss lemma guarantees that:

\(P\left[\text{error} >\epsilon\right]\leq e^{-\gamma\epsilon^2 k}.\)

This means that the probability that we choose E such that the error is greater than 𝛜 is bounded by exp(-𝝲𝛜²k), where 𝝲 is just a scaling constant. If we choose k → ∞, then P[error > 𝛜] → 0 for any 𝛜. A good choice is k ~ log N / 𝛜², yielding:

\(P\left[\text{error} >\epsilon\right]\leq N^{-\gamma}.\)

This means that we can choose an arbitrarily small 𝛜 such that P[error > 𝛜] → 0 as the sequence length increases N → ∞. Understand this as a mere theoretical guide that tells us that choosing k ~ log N will guarantee smaller errors as N increases. In practice, k is chosen independently of N, leading to the O(N) linear complexity while accepting the cost of the approximation error. Additionally, E is chosen as a parameter layer for the model to learn. For example, they showed that choosing k = 64 with N = 512 leads to slightly worse performance than the full attention.

Since the attention matrix has dimension N x k, we also need to project the values:

\(C = \text{Softmax}\left(\frac{Q^\top EK}{\sqrt{d}}\right)FV\)

where F is the N x k projection matrix for the tensor V. As for E, F is also learned during training.

Projecting the keys and values EK, FV leads to complexity O(Nk). Computing the alignment scores Q^TEK and the context vectors C = AFV are also following O(Nk). Since we fix k, the overall time and space complexity is O(N).

Recurrent Attention Equivalence: The Linear Transformer

So far, we have accepted the attention mechanism to be represented by the following computation:

\(\begin{align} C &= \text{Softmax}\left(\frac{Q^\top K}{\sqrt{d}}\right)V \quad \text{or}\nonumber\\ \mathbf{c}_i &= \frac{\sum_{j=1}^N \exp\left(\frac{\mathbf{q}_i^\top \mathbf{k}_j}{\sqrt{d}}\right) \mathbf{v}_j}{\sum_{j=1}^N \exp\left(\frac{\mathbf{q}_i^\top \mathbf{k}_j}{\sqrt{d}}\right)} \quad \text{for individual vectors} \end{align}\)

However, this specific analytical choice is not the only one that could be chosen to fulfill the same functional role in capturing pairwise interactions between tokens. Let's review the roles of the different elements in this equation:

• The dot-product Q^TK: Similarity computation. For each query vector, it tells you how "compatible" or similar it is to each key vector. This yields a matrix of unnormalized attention scores.

• Normalizing by √d: Variance control. The primary purpose of scaling by √d is to control the scale of the attention logits before softmax, ensuring stable gradient flow and preventing the softmax from becoming too "confident" (peaked). Furthermore, extremely large logits can cause numerical instability (e.g., NaN in floating-point arithmetic), and scaling mitigates this.

• Softmax operation: Normalization and nonlinearity. The softmax turns the unnormalized similarity scores into a probability distribution, amplifying the effect of the most relevant keys.

• Multiplication by V: Weighted aggregation. Each output is a weighted sum of the values, where the weights come from the normalized similarity scores. This is how the model “mixes” information from across the input sequence.

Functionally, we need a similarity function sim that is non-linear and captures the pairwise token interaction:

\(\mathbf{c}_i = \frac{\sum_{j=1}^N \text{sim}(\mathbf{q}_i, \mathbf{k}_j) \mathbf{v}_j}{\sum_{j=1}^N \text{sim}(\mathbf{q}_i, \mathbf{k}_k)}\)

where the denominator ensures that the similarity function is normalized to 1. If we choose sim(q_i, k_j) = exp(q_i^Tk_j / √d), we recover the softmax transformation. The Linear Transformer proposed a new attention mechanism with a different analytical form, but with similar functional roles. More specifically, they suggested a similarity function where we can factorize the contribution from the keys and the queries as a product:

\( \text{sim}(\mathbf{q}_i, \mathbf{k}_j)=\phi(\mathbf{q}_i)^\top\phi(\mathbf{k}_j).\)

In the context of kernel methods in machine learning, ɸ is called a "feature map". A feature map is a function that transforms an input vector into a new space, often a higher-dimensional one, so that a kernel function (which measures similarity) can be expressed as an inner product in that space. Essentially, ɸ extracts or "maps" the original features into a new representation where the desired similarity (that mimics the softmax behavior) is computed simply by taking a dot product. In the context of the Linear Transformer, they simply chose ɸ as follows:

\( \phi(x) = \begin{cases} x+ 1 & \text{if } x > 0, \\ \exp x & \text{otherwise}. \end{cases}\)

This ensures that sim(q_i, k_j) is always positive and is computationally stable while being non-linear. The main appeal of this linearization of the similarity kernel is the associativity property of the matrix multiplication:

\(\mathbf{c}_i = \frac{\sum_{j=1}^N \phi(\mathbf{q}_i)^\top\phi(\mathbf{k}_j)\mathbf{v}_j}{\sum_{j=1}^N\phi(\mathbf{q}_i)^\top\phi(\mathbf{k}_j)}=\frac{ \phi(\mathbf{q}_i)^\top\sum_{j=1}^N \phi(\mathbf{k}_j)\mathbf{v}_j^\top}{\phi(\mathbf{q}_i)^\top\sum_{j=1}^N \phi(\mathbf{k}_j)}\)

For one key and one query, ɸ(q_i)^Tɸ(k_j) takes d operations. Multiplying the resulting scalar alignment score to v_j takes another d operations. Therefore, for all the keys, computing ∑ɸ(q_i)^Tɸ(k_j)v_j takes 2Nd operations, and the time complexity is O(Nd) per query. Similarly, the denominator ∑ɸ(q_i)ɸ(k_j) follows a time complexity of O(Nd). Because we have N queries, the total cost is

\( \mathcal{O}(N^2d_\text{model})\quad \text{(our typical quadratic complexity!).}\)

If we consider the multiplications in a different order, ɸ(k_j)v_j^T is an outer product and results in d² operations. For N keys and values, we end up with Nd² operations for ∑ɸ(k_j)v_j^T. In the denominator, summing the different keys ∑ɸ(k_j) requires Nd operations. Let's call S = ∑ɸ(k_j)v_j^T and z = ∑ɸ(k_j). S is a matrix of size d x d and z is a vector of size d. Computing ɸ(q_i)^TS brings another d² operations, and computing ɸ(q_i)^Tz takes d operations. Therefore, the cost of ɸ(q_i)^TS / ɸ(q_i)^Tz per query is O(d² + d) = O(d²). For N queries, we obtain a total complexity of: