How To Reduce LLM Decoding Time With KV-Caching!
The attention mechanism is known to be pretty slow! If you are not careful, the time complexity of the vanilla attention can be quadratic in the number of tokens in the input sequence! So, we need to be smart about the computations we are doing when we are decoding text sequences. When we decode text, there are actually many tensors that we recompute over and over, so instead of recomputing them, we are going to cache them to save on computation. Let me show you how!
When you use ChatGPT or Claude, why does the first token take longer to appear than the second one? That is thanks to KV caching!
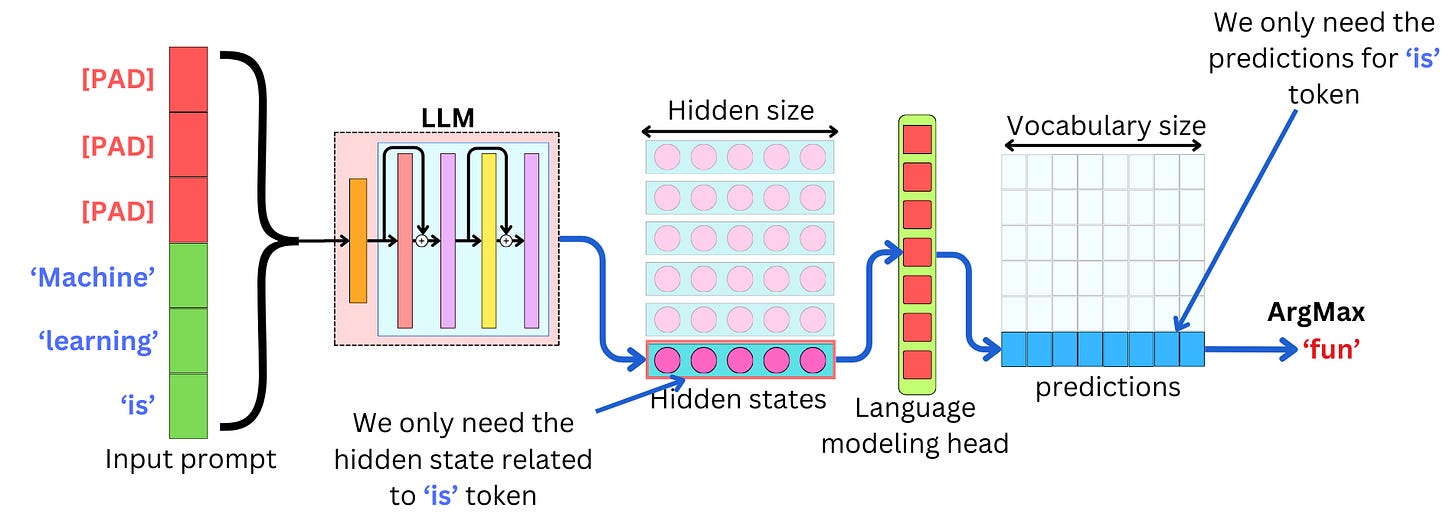
An LLM generates text by iteratively predicting the next token and appending it to the previously generated tokens and the original prompt. Typically, causal LLMs are trained to predict the next word in the sequence. This means that each input token maps to a resulting hidden state within the Transformer, which in turn maps to a prediction vector for the following token. The prediction vector has as many predictions as there are tokens in the dictionary, and the next token can be predicted by greedily finding the prediction with the highest probability. This means that when we are decoding a specific token, we only need to compute its corresponding hidden state and discard the others.
This required hidden state corresponds to the last token of the input sequence. To compute this hidden state in each of the self-attention layers, we need all the Keys and Values of the whole input sequence but only the Query for the last token of this sequence. We generate the attentions for the last token by taking the Softmax of the dot product between the Query and all the Keys:
And we get the resulting hidden state by taking the weighted average of all the Values as given by the attentions:
There are a few conclusions that we can draw. First, there is no need to compute attentions besides the ones corresponding to the last token. This means that during the decoding process, the time complexity at each iteration is linear in the number of input tokens (~O(N)), even with a vanilla attention mechanism. Second, the Keys and Values remain the same for each of the tokens for all iterations. This means that we don't need to recompute them at every iteration. That is where the idea of KV caching comes from!
The decoding process can be divided into 2 phases: the initialization phase and the generation phase. In the initialization phase, all the Keys and Values corresponding to all the tokens in the input prompt need to be created. This takes almost as long as the following phase. We can then store all the keys and values for all the attention layers in the KV cache. In the generation phase, we only need to generate the Key, Query, and Value corresponding to the last token in the input sequence. We can then pull the stored Keys and Values from the cache to compute the required hidden states. In the end, we update the cache with the latest computed Key and Value corresponding to that last token.
This KV caching process significantly reduces the latency associated with text generation!
The problem with the typical KV-cache implementation is that the memory gets pre-allocated to the maximum output size of the model. This means that the allocated memory cannot be used by another process.
It makes KV-caching fast but very inefficient if multiple sequences need to be decoded at once. For example, allocating memory for a Llama 3 model takes more than 10 GB of memory.
The paged-attention algorithm is a way to allocate memory in chunks when needed instead of the full output size, which allows more parallel decoding processes at once.