Transforming Text Into Tokens: The WordPiece VS The Byte Pair Encoding Algorithm

• The WordPiece tokenization algorithm

• The Byte Pair Encoding Strategy

---

The live Machine Learning Fundamentals Bootcamp starts February 12th!

Subscribers to the AiEdge Newsletter get a 20% discount by applying the following coupon: NEWSLETTER

---

The WordPiece tokenization algorithm

The WordPiece algorithm is a subword tokenization algorithm that was initially developed by Google for use in neural machine translation in 2012 and later popularized by models like BERT in 2018. Tokenization is the feature engineering of natural language processing, and the goal of WordPiece is to find the "best" features!

We are going to create a toy example to illustrate the mechanisms of this algorithm. Let's assume we have very simple training data composed of four text sequences {'low', 'lower', 'newest', 'widest'}. We want to find consecutive groups of letters that can be used as tokens. At first, we are going to assume that the tokens are just the single characters themselves:

• [_, l, o, w]

• [_, l, o, w, e, r]

• [_, n, e, w, e, s, t]

• [_, w, i, d, e, s, t]

The character '_' is just a special character used as a marker to indicate the beginning of a word. The current vocabulary capturing that character-level tokenization is just:

\( \texttt{\{_, l, o, w, e, r, n, s, t, d\}}\)

A typical strategy to guide the quality of a modeling choice is the likelihood maximization principle computed on the training data. The likelihood, in this context, is just the product of the text sequence probabilities:

\(\begin{equation} \begin{split} \mathcal{L} = & P(\texttt{_,l,o,w}) \times \\ & P(\texttt{_,l,o,w,e,r}) \times \\ & P(\texttt{_,n,e,w,e,s,t}) \times \\ & P(\texttt{_,w,i,d,e,s,t}) \end{split} \end{equation}\)

We would like to group together characters that tend to co-occur often in the training data or, probabilistically speaking, characters that depend on each other. If A and B are two probabilistic events, we say that A and B are independent if:

\(P(A,B)=P(A)P(B)\)

and conversely, they are dependent if

\(P(A,B)\neq P(A)P(B).\)

If we have P(A,B) > P(A)P(B), it means that A and B are more likely to co-occur than random chance would predict. Currently, with our simple character-level tokens, we are implying independence of the different characters:

• P(_,l,o,w)=P(_)P(l)P(o)P(w)

• P(_,l,o,w,e,r)=P(_)P(l)P(o)P(w)P(e)P(r)

• P(_,n,e,w,e,s,t)=P(_)P(n)P(e)P(w)P(e)P(s)P(t)

• P(_,w,i,d,e,s,t)=P(_)P(w)P(i)P(d)P(e)P(s)P(t)

To find better tokens, we need to be able to estimate those probabilities. The most basic approach is to count the tokens. For example, for the character e:

\(P(\texttt{e}) \simeq \frac{\text{Freq}(\texttt{e})}{N}=\frac{4}{24}\)

Where Freq(e) is the number of occurrences of the character e, and N is the total number of tokens. Let's now consider all the pairs of consecutive characters in the training data:

\( \texttt{\{_l, lo, ow, we, er, _n ,ne, ew, es, st, _w, wi, id, de\}} \)

Again, to estimate the probabilities associated with those pairs, we count the occurrences. For example, for the pair lo:

\(P(\texttt{lo}) \simeq \frac{\text{Freq}(\texttt{lo})}{N_{\text{pairs}}}=\frac{2}{20} \)

Here, N_pairs = N-4 represents the number of continuous pairs of characters in the training data, where 4 is the number of text sequences of our toy example. How does that compare to P(l)P(o)?

\(P(\texttt{l})P(\texttt{o}) \simeq \frac{\text{Freq}(\texttt{l})} {N} \frac{\text{Freq}(\texttt{o})}{N}=\frac{2}{24} \times \frac{2}{24}=\frac{1}{144}\)

So P(lo) > P(l)P(o) and the pair lo is a good token candidate to increase the likelihood because

\( P(\texttt{_,lo,w}) P(\texttt{_,lo,w,e,r}) > P(\texttt{_,l,o,w}) P(\texttt{_,l,o,w,e,r}\)

To maximize the likelihood as much as possible, we actually want to find the pair of characters a and b that maximize the ratio P(ab) / (P(a)P(b)) as long as it is greater than 1.

The algorithm starts to emerge! We can iteratively find the pair of tokens that maximizes the likelihood the most and add that pair of tokens as a new token into the vocabulary until the vocabulary is large enough. Let's go through a few iterations of this process to help us visualize better.

First iteration

Step 1. We start with the character-level tokenization:

• [_, l, o, w]

• [_, l, o, w, e, r]

• [_, n, e, w, e, s, t]

• [_, w, i, d, e, s, t]

with initial token dictionary:

\( \texttt{\{_, l, o, w, e, r, n, s, t, d\}} \)

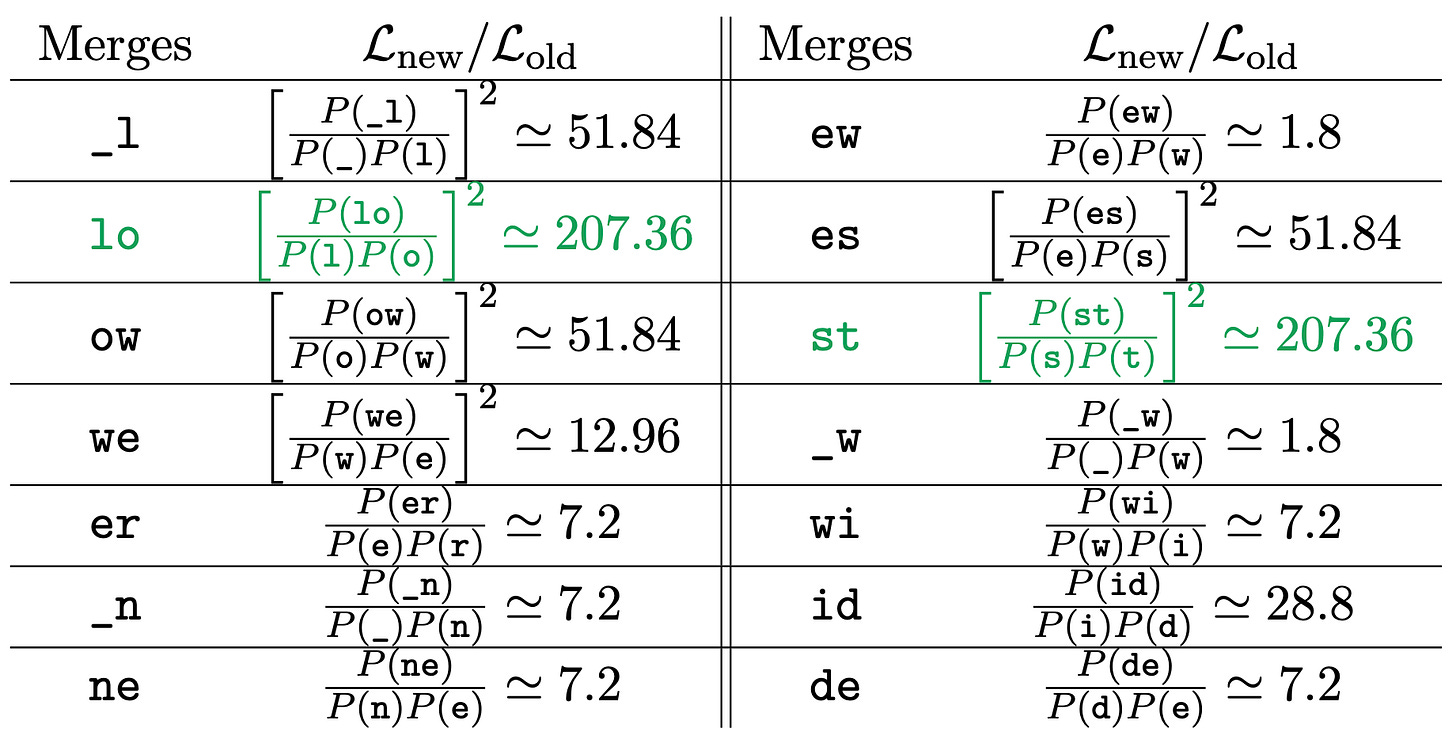
Step 2. We compute the ratio L_new / L_old for all the possible merges of pairs of consecutive tokens. Because the likelihood is multiplicative, the ratio simplifies to:

\( \left.\frac{\mathcal{L}_{\text{new}}}{\mathcal{L}_{\text{old}}}\right\vert_\texttt{lo}=\left[\frac{P(\texttt{lo})}{P(\texttt{l})P(\texttt{o})}\right]^2\)

when we merge the characters lo. For all the possible merges:

We see that the best merge candidates for likelihood increase are lo and st. In the case where we have two candidates with the same likelihood increase, we can always have a heuristic rule to make a deterministic choice. Let's choose the first one in alphabetical order: lo.

Step 3. We update the token dictionary with the new merged token:

\( \texttt{\{_, l, o, w, e, r, n, s, t, d, lo\}} \)

and we adapt the tokenization to account for the new token:

• [_, lo, w]

• [_, lo, w, e, r]

• [_, n, e, w, e, s, t]

• [_, w, i, d, e, s, t]

Second iteration

Step 1. We start from the current tokenization and dictionary.

Step 2. We compute the ratio L_new / L_old for all the possible merges of pairs of consecutive tokens.

st is the best merge candidate.

Step 3. We update the token dictionary with the new merged token:

\( \texttt{\{_, w, e, r, n, s, t, d, lo, st\}} \)

and we adapt the tokenization to account for the new token:

• [_, lo, w]

• [_, lo, w, e, r]

• [_, n, e, w, e, st]

• [_, w, i, d, e, st]

The process is straightforward, and we can iterate as many times as we wish. Let's summarize the algorithm:

1. We start with character-level tokenization

2. We compute L_new / L_old for all the possible merges of pairs of consecutive tokens.

3. We merge the token that maximizes the likelihood.

4. Repeat the process until you reach the desired number of merges.

By applying this algorithm, we could continue the merging process and progressively add more tokens to the dictionary:

• 3rd iteration: We add _lo to the dictionary:

  \(\texttt{[_lo, w]}, \texttt{[_lo, w, e, r]}, \texttt{[_, n, e, w, e, st]}, \texttt{[_, w, i, d, e, st]} \)

• 4th iteration: We add id to the dictionary:

  \( \texttt{[_lo, w]}, \texttt{[_lo, w, e, r]}, \texttt{[_, n, e, w, e, st]}, \texttt{[_, w, id, e, st]}\)

• 5th iteration: We add _low to the dictionary:

  \(\texttt{[_low]}, \texttt{[_low, e, r]}, \texttt{[_, n, e, w, e, st]}, \texttt{[_, w, id, e, st]} \)

• 6th iteration: ...

The original BERT-Base and BERT-Large had a final vocabulary of ~30,000 tokens.

The Byte Pair Encoding Strategy

The Byte Pair Encoding (BPE) was originally proposed as a data compression algorithm in 1994 by Phil Gage. It was later suggested as a subword tokenization process for neural machine translation in 2016. In practice, it is actually very similar to, and even simpler than, the WordPiece algorithm. It is now the standard tokenization strategy in most modern large language models (GPT 1-4, Llama 1-3, ...). Instead of choosing the merges that maximize the likelihood measured on the training data, we simply choose the ones with the highest frequencies. Let's look at the first iteration of the algorithm: