Understanding How LoRA Adapters Work!
LLM Fine-Tuning
LoRA Adapters are, to me, one of the smartest strategies used in Machine Learning in recent years! LoRA came as a very natural strategy for fine-tuning models. In my opinion, if you want to work with large language models, knowing how to fine-tune models is one of the most important skills to have these days as a machine learning engineer.
Watch the video for the full content!
One very strong strategy to fine-tune LLMs is to use LoRA adapters. LoRA adapters came as a very natural strategy for fine-tuning models. The idea is to realize that any matrix of model parameters in a neural network of a trained model is just a sum of the initial values and the following gradient descent updates learned on the training data mini-batches.
From there, we can understand a fine-tuned model as a set of model parameters in which we continue to aggregate the gradients further on some specialized dataset.
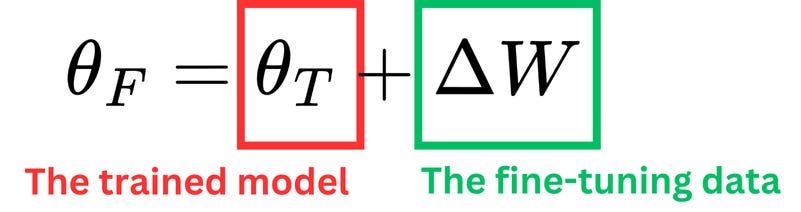
When we realize that we can decompose the pretraining learning and the fine-tuning learning into those two terms
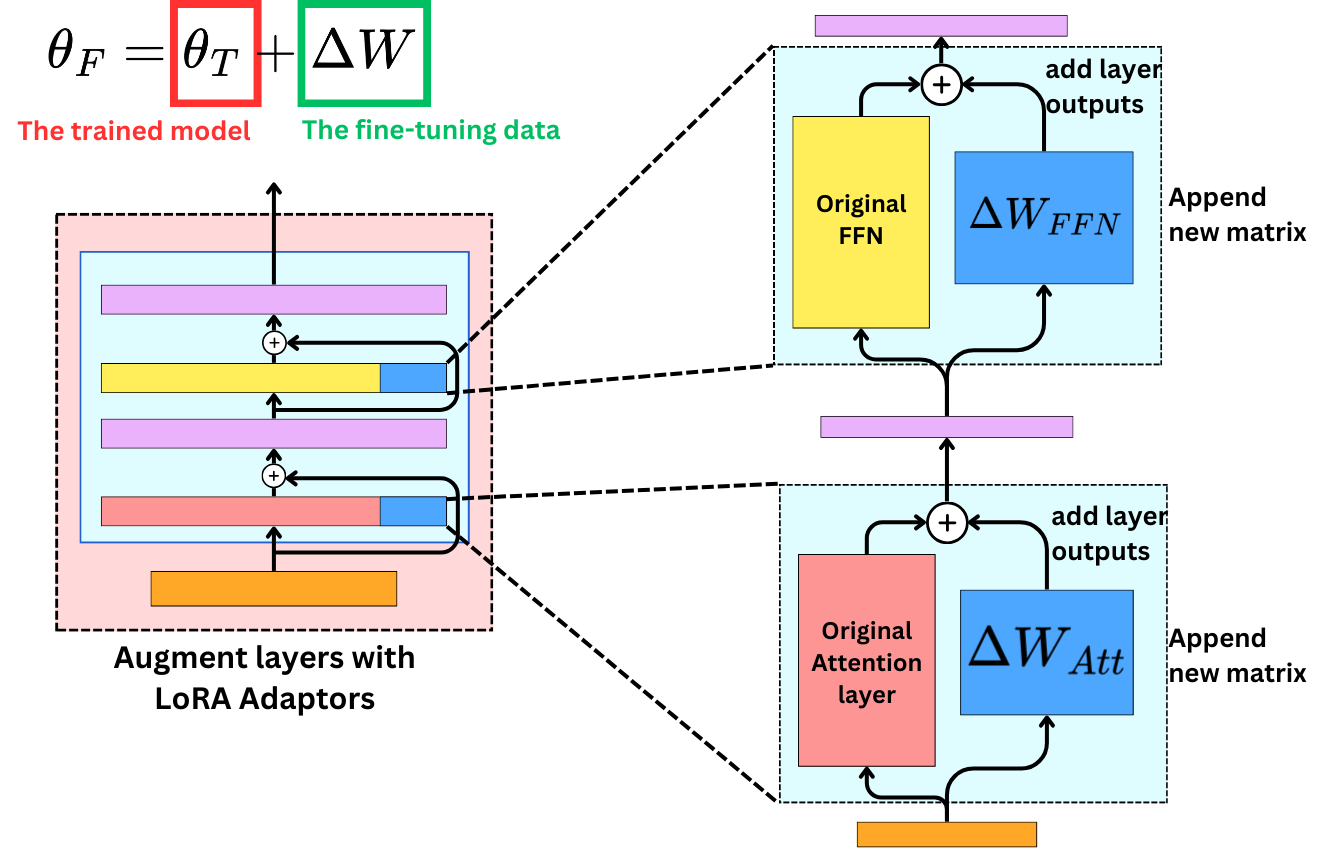
then we understand that we don't need that decomposition to happen into the same matrix; we could sum the output of two different matrices instead. That is the idea behind LoRA: we allocate new weight parameters that will specialize in learning the fine-tuning data, and we freeze the original weights.
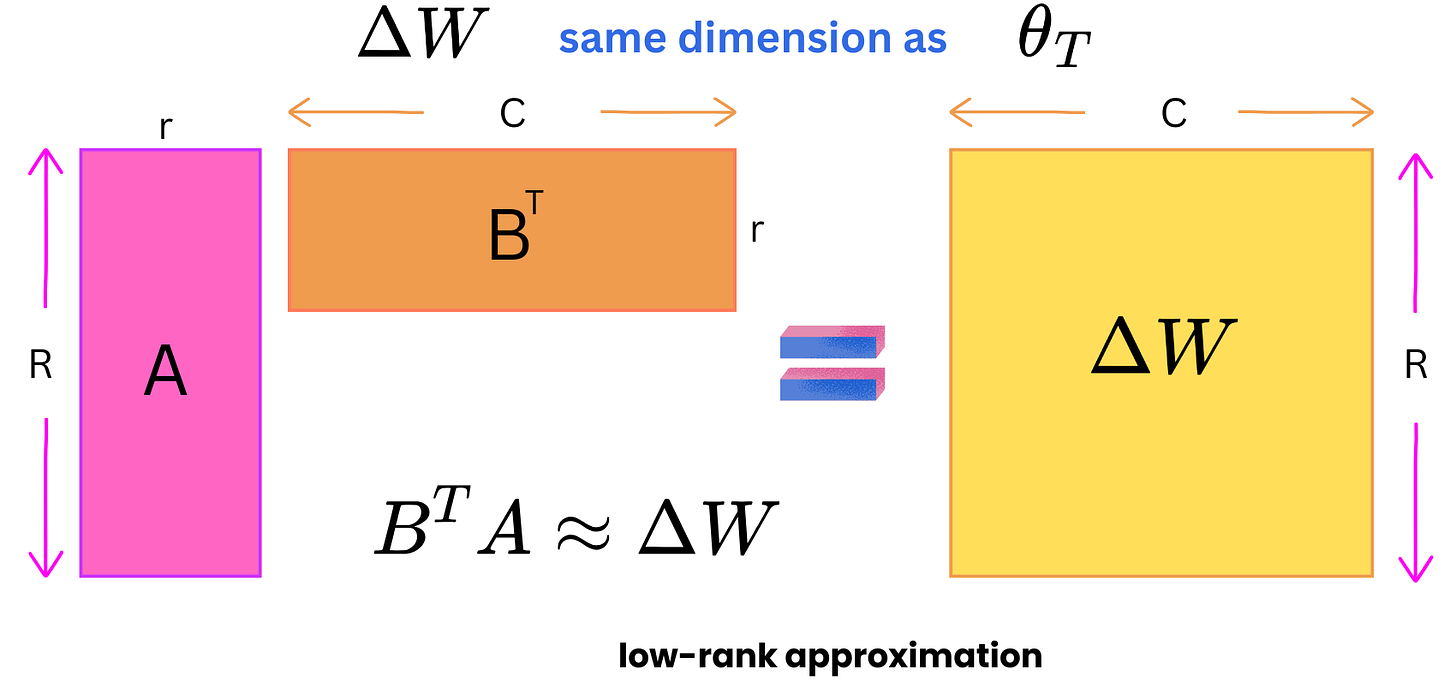
As such, it is not very interesting because new matrices of model parameters would just double the required memory allocated to the model. So, the trick is to use a low-rank matrix approximation to reduce the number of operations and required memory. We introduce 2 new matrices, A and B, to approximate ΔW.
In the forward pass, we use the original weights and the new adapters to compute the hidden states.
However, during the backward pass, we only need to compute the gradients for the adapters as they are the weights that are being trained.
The trick is that if ΔW has dimensions (R, C), we can create B with dimensions (R, r) and A with dimensions (r, C) such that r << R, C. For example if R = 10K, C = 20K and r = 4, then:
ΔW has R x C = 10K x 20K = 200M elements
B has R x r = 10K x 4 = 40K elements
and A has r x C= 20K x 4 = 80K elements
Therefore A and B combined have 120K elements which is 1666 times less elements than ΔW. When we fine-tune, we only update the weights of those newly inserted matrices. The gradient matrices are much smaller and therefore require much less GPU memory space. Because the pre-trained weights are frozen, we don't need to compute the gradients for a vast majority of the parameters.
SPONSOR US
Get your product in front of more than 64,000 tech professionals.
Our newsletter puts your products and services directly in front of an audience that matters - tens of thousands of engineering leaders and senior engineers - who have influence over significant tech decisions and big purchases.
To ensure your ad reaches this influential audience, reserve your space now by emailing damienb@theaiedge.io.



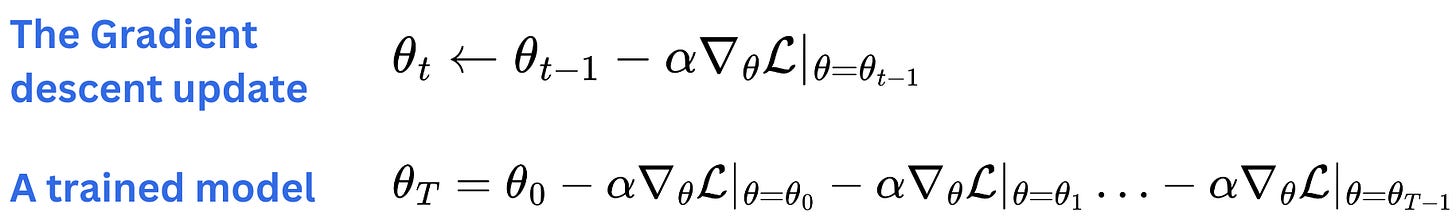

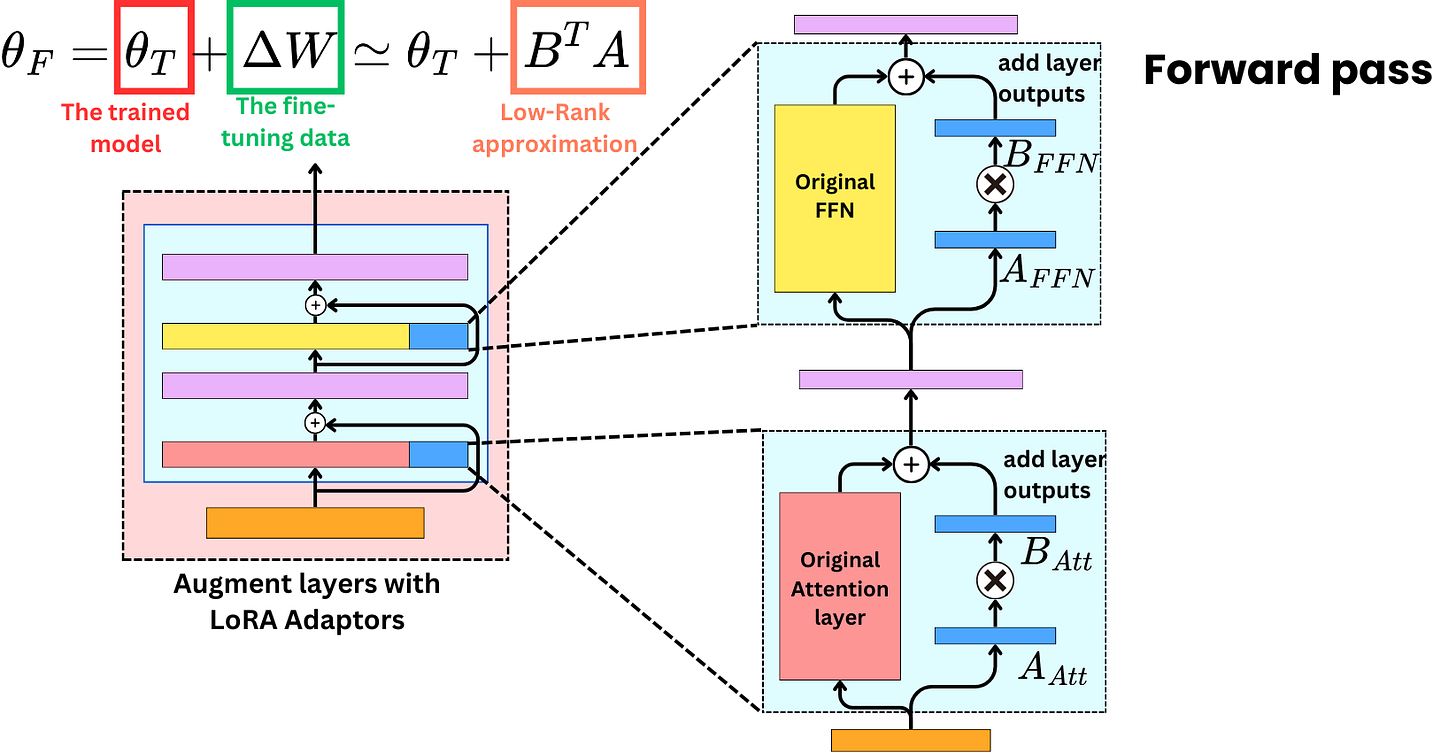
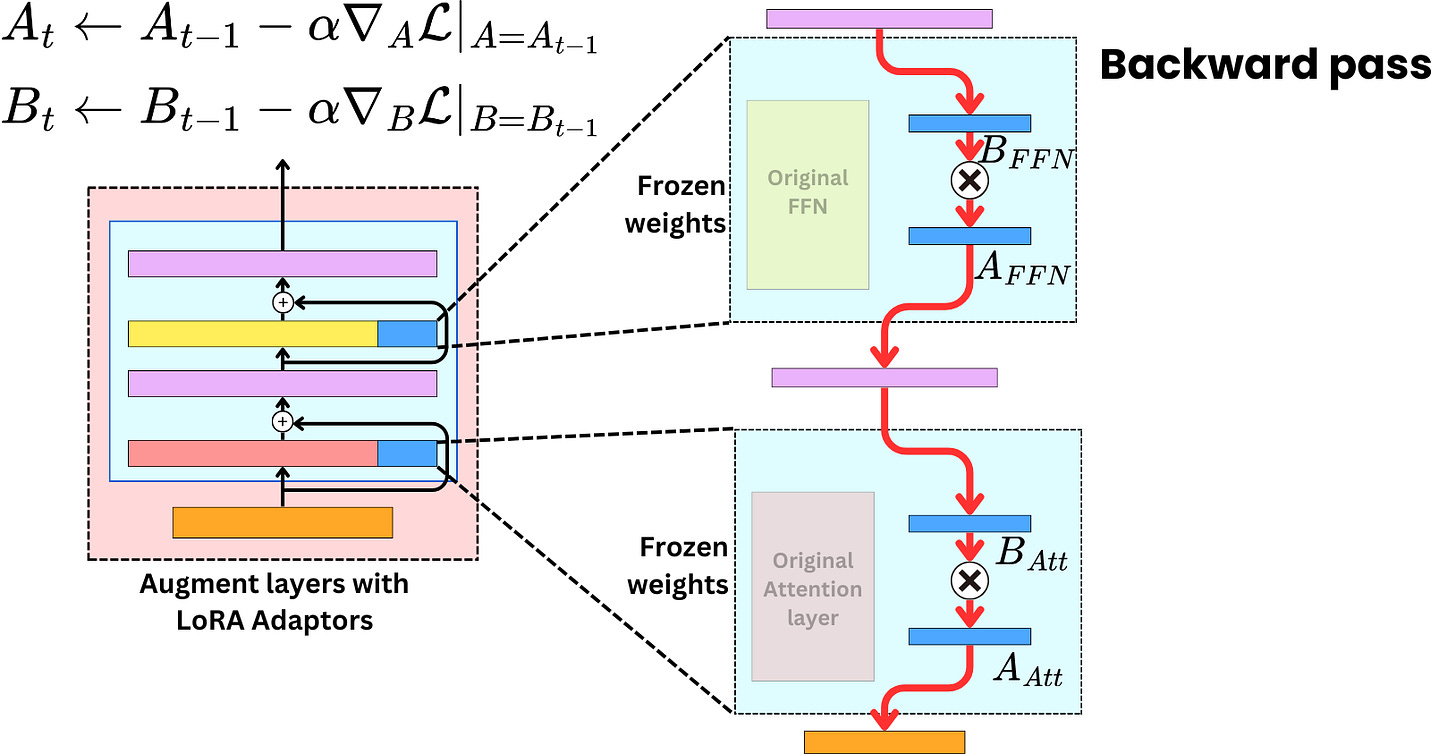

LoRA is a very important algorithm in PEFT and also an algorithm that I have found to be very effective in practice when training LLM models. LoRA is not complex but is very cleverly designed: firstly, LoRA does not increase any inference time. Secondly, LoRA does not change the original model but only trains an additional new parameter, and this parameter is only used to adapt to the current task. However, this also means that LoRA needs multiple different ΔW when training for multiple tasks, and learning multiple tasks is relatively difficult for LoRA, unless they are treated as the same task.