Deep Dive: How Uber Predicts Arrival Times with Deep Learning

Machine Learning System Design

---

How does Uber predict ride ETAs? ETAs are used to compute fares so it is critical to be quite accurate. We present in this letter DeeprETA, a low-latency deep neural network architecture for global ETA prediction developed by Uber. We look at:

• The overall architecture

• The routing engine ETA

• The model

• The data

• The training and serving pipeline

---

Overview

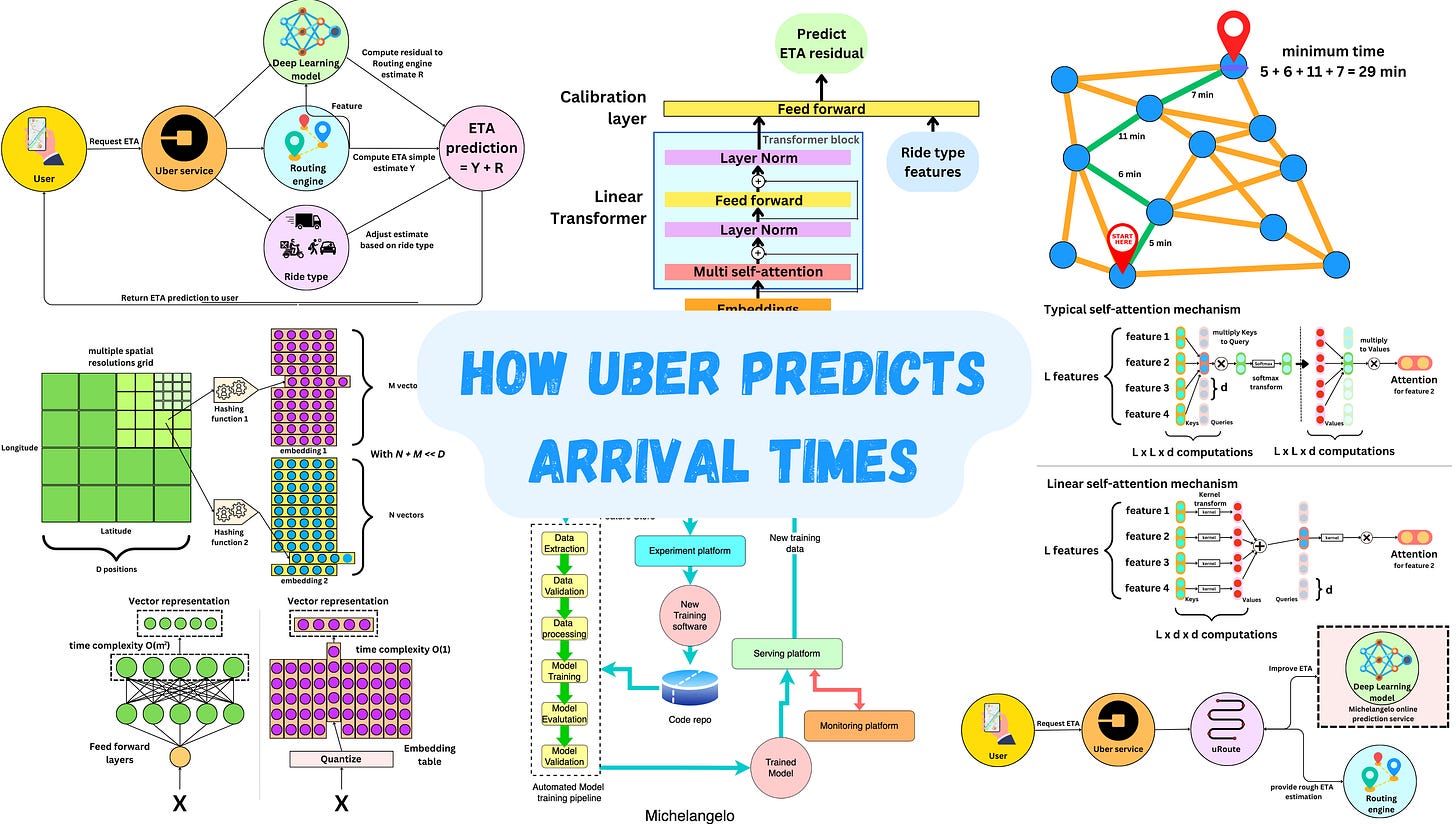
The Expected Time of Arrival (ETA) process starts when a user looks for a ride on the application. An ETA is provided to the user and used to calculate the ride's fares. The process is as follows:

1. The user requests an ETA from the mobile application and it is sent to the Uber service

2. The Uber service calls a routing engine to provide a rough ETA estimate.

3. Uber uses a Deep Learning model that refines the routing engine estimate. The routing engine computes an estimate Y and the Deep Learning model computes the residual R of Y such that Y + R is a better estimate. So the target the model is learning is

   \(R = \text{Ground truth ETA} - Y\)

4. The model’s predictions are refined by considering the ride type (delivery trips vs ride trips, long vs short trips, pick-up vs drop-off trips).

5. The prediction is served to the user in a few milliseconds.

There are some critical requirements for this system:

• The latency must be very low! We will need to reduce the capacity of the model if its inference time is too low.

• It must be accurate! Despite the latency requirements, we aim for the most optimal model possible under those constraints.

• It must be general! It has to adapt to very different use cases. User ride ETAs and delivery ETAs, for example, differ greatly.

The Routing Engine ETA

The process

Think of the routing engine as Uber's version of Google Maps. Why can’t the routing engine be enough? The routing engine just computes the time to get from A to B, but an Uber ride is a bit more than that. We need to consider the different drivers available near by for the ride. We need to account for the difficulty for parking in the pick up location or destination. Moreover, the routing engine is probably not completely real-time, and the machine learning model will be able to use real-time traffic information.

A routing engine works as follows:

• The different road segments and intersections work as a graph. The intersections are the nodes and the road segments are the edges connecting them.

• Based on current traffic information and historical data, we produce a time estimate to go from one node to another neighboring node. Each road segment receives an edge weight matching those time estimates.

• We can now use graph algorithms to find the path that minimizes the total time to travel from the pick location to the destination.

The A* search algorithm

A typical path search algorithm is the A* search algorithm and it is likely that most routing engines utilize custom versions of it. We iteratively explore the graph in a Best-first search manner by taking paths that (1) minimize the time spent from the origin and (2) the distance to the destination. To compute the distance to the destination, we can use the Haversine distance formula with the latitude and longitude values. The algorithm stops when the destination is reached. It is fast but it is only an approximation to the optimal solution as we avoid exploring all possible paths and focus only on the most promising. Here is the pseudo-code

nodes_to_explore = []
explored_nodes = []

# initiate the value attribute of the node
start_node.value = 0
# we start from the starting node
nodes_to_explore.append(start_node)

while nodes_to_explore:

    # get the node with smallest value
    node = nodes_to_explore.pop_smallest_value()
    explored_nodes.append(node)

    # if we reached the goal, we can return the whole path
    if node is goal:
        return 'goal reached'
    
    # else we explore the children of the current node
    for child in node.children:
        if child in explored_nodes:
            continue
        
        child.time_from_start = node.time_from_start + time_to_child
        child.distance_to_end = distance from child to end

        # the node's value is the key metric of the problem!
        # We want to take the path that both minimize the time
        # from the starting point and is closer to the end point.
        # By minimizing on the value, to take a good guess on the 
        # next node to explore first.
        child.value = child.time_from_start + child.distance_to_end 
        nodes_to_explore.append(child)

The model

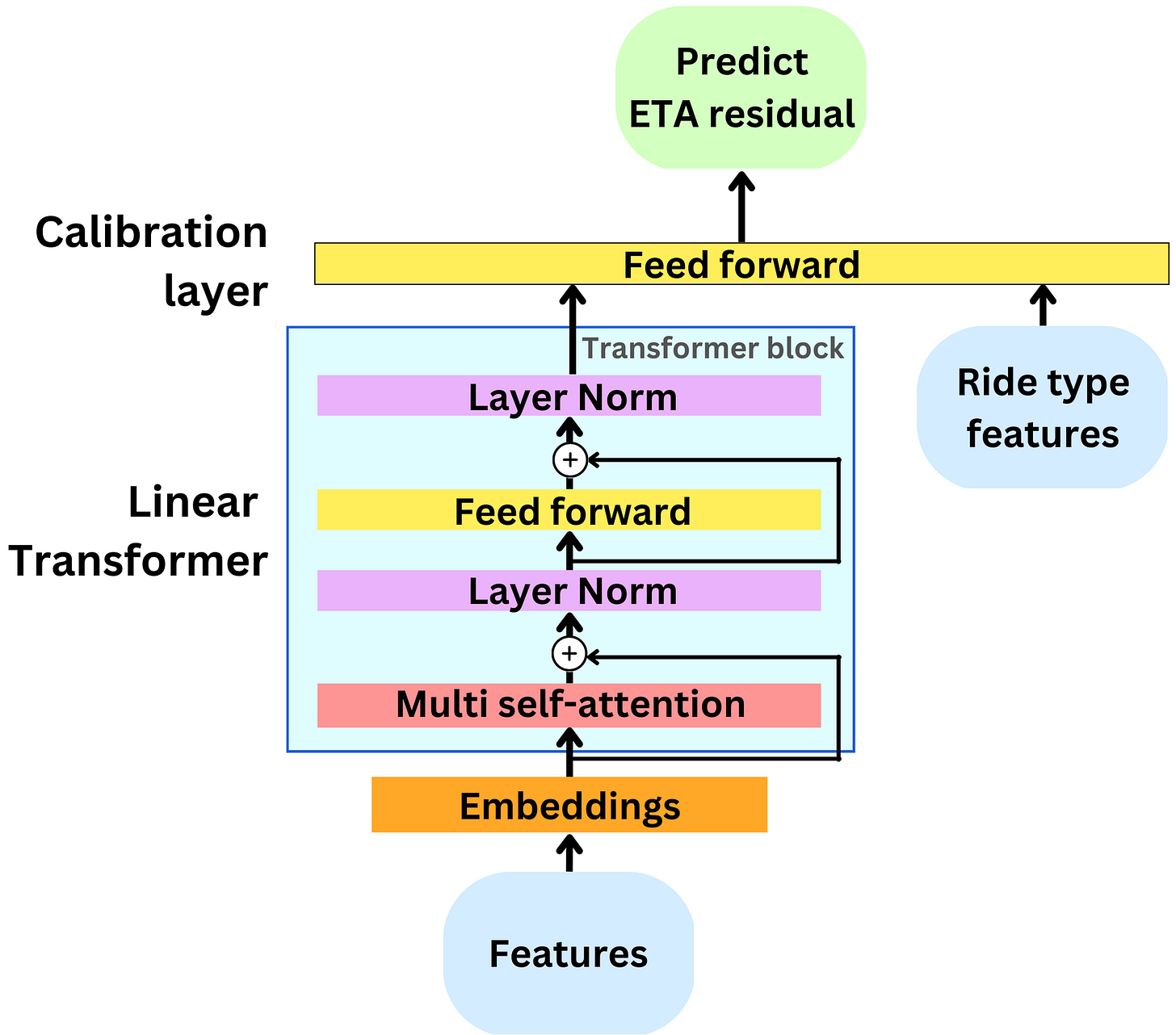
The model consists of a Linear Transformer (“Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention”) block followed by a feed forward network. The Transformer block takes in most of the features where the calibration layers look at the Transformer output and the ride type features on the same footing. This is such that those are considered with more attention by the model.

The Linear Transformer