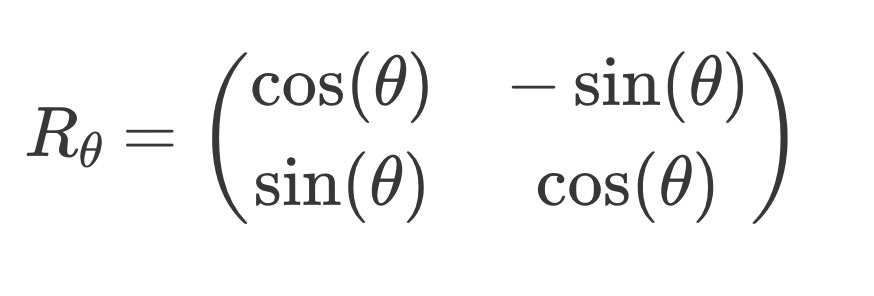How to Fine-Tune LLMs for Larger Context Size with LongLoRA

Fine-tuning LLMs to increase their context size is not a trivial task, as the time complexity of training and inference increases quadratically with the number of tokens in the input prompt. I am reviewing here a strategy developed in LongLoRA to minimize the training time while keeping the model performance high.

• Understanding the RoPE embedding

• Extending the context size

• Creating sparse Attention layers

• Fine-tuning with LoRA

---

One trend that seems hard to stop is the expansion of the context size (maximum number of tokens) for open-source and close-source Large Language Models. When BERT came out in 2018, its default context size was 512. When ChatGPT came out in 2022, its context size was 2048 to 4096 tokens. Now, the default context size for OpenAI models is 128K tokens, 200K for the Anthropic models, and ~1M for the Gemini models. So how do we train a large language model to have a large context window?

Training with a large context window can be tricky because of the attention mechanism. The vanilla attention mechanism has a space and time complexity of O(N²), where N is the number of input tokens. For example, if you fine-tune Llama models, they use a full attention mechanism that might lead to long training times.

One strategy that has been suggested in the LongLoRA paper is to modify the position encoding and then the attention layers to induce sparsity in the attention computation. Let’s dig into that strategy.

Understanding the RoPE embedding

Most modern LLMs are built using the RoPE (Rotary Position Embedding) positional encoding. It offers a couple of advantages compared to the typical positional encoding:

• Relative Position Encoding: RoPE dynamically encodes relative positions through rotations, enabling models to capture sequence relationships without relying on static, absolute positional embeddings.

• Generalizes to Variable Sequence Lengths: Unlike traditional embeddings, RoPE naturally adapts to sequences of varying and unseen lengths, improving model flexibility and generalization.

• Parameter Efficiency: RoPE integrates positional information without additional learnable parameters, making it an efficient approach that simplifies model architecture.

• Improved Interpretability: The methodical integration of positional information through RoPE enhances the interpretability of how position influences attention and model decisions.

• Support for Infinite Sequences: RoPE's mathematical foundation allows for handling theoretically infinite sequence lengths, limited only by computational constraints, not architectural ones.

In the original Transformer architecture, we were adding a positional encoding to the semantic embeddings:

Here you can check this newsletter, where I explain how the original position encoding was designed:

The idea of RoPE is that instead of adding a positional encoding to the semantic embeddings, we are going to rotate the keys and queries in attention layers based on the position of the related tokens in the input sequences:

This will lead to the attentions containing the positional information. The values are NOT rotated, though. Therefore, the rotations only affect the weighted averages when we are performing the tensor operation between the values and the self-attentions.

To rotate a 2D vector V with an angle 𝜭, we just need to apply the rotation matrix R_𝜭:

with V' being the new vector:

\(V'=R_\theta V\)

So the trick is to find a way to apply that rotation to the keys and queries. Instead of extending this operation to vectors of higher dimensions, RoPE simply breaks down the vectors into pairs of elements and applies a pairwise 2D rotation to each of the pairs of elements:

For those rotations, the angle is not only dependent on the position p of the related token but also on the position k of the rotated segment within the vector. To make it simpler, we usually have 𝜭_pk = p𝜭_k. So the whole rotation matrix becomes: