All About The Modern Positional Encodings In LLMs

The Positional Encoding in LLMs may appear somewhat mysterious the first time we come across the concept, and for good reasons! Over the years, researchers have found many different ad-hoc ways to encode positions and relative positions in the attention mechanism. The most recent surprise to me is the emergence of NoPE (no positional encoding) as being better for generalization on longer sequences. Today, we look at:

• Additive Relative Positional Embeddings

• Multiplicative Relative Positional Embeddings

• ALiBi: Attention With Linear Biases

• RoPE: Rotary Position Embedding

  • The Complex Number Representation

  • Increasing The Context Window With RoPE

• No Position Encoder: NoPE

  • How NoPE Can Learn Relation Positional Information

  • Better Generalization for Longer Distance

  • Llama 4's iRoPE

---

The original positional encoding scheme introduced in "Attention is All You Need" uses sinusoidal functions to create absolute position representations, but this approach revealed significant shortcomings when handling longer sequences or transferring to different sequence lengths:

• Fixed context windows and poor extrapolation: When faced with sequences longer than this predefined limit, the model must either truncate the input or use positional values it never encountered during training. Perhaps the most significant limitation is that vanilla encodings represent absolute positions rather than relationships between tokens.

• The absolute vs. relative position problem: In language, relative positions often matter more than absolute ones. Consider the sentence: "The dog that chased the cat ran away." The relationship between "dog" and "ran" remains the same whether this is the opening sentence of a document or appears on page fifty, but absolute encodings fail to directly capture this invariance.

• Information dilution through layers: As signals propagate through the multiple layers of a Transformer, the influence of the original positional information tends to weaken. The model must work harder to maintain positional awareness in deeper layers, especially for distant tokens.

• Limited inductive bias for local relationships: Natural language exhibits a locality bias as nearby words often have stronger relationships than distant ones. The vanilla encoding doesn't naturally encode this bias, treating position 5 and position 500 as equally valid attention targets from a structural perspective, requiring the model to learn this pattern from data alone.

• Mathematical constraints: The sinusoidal functions used in the original formulation were chosen partly for their theoretical ability to generalize to unseen positions. However, in practice, they still struggle with significant extrapolation beyond the training range. The model learns to associate specific patterns with specific position ranges, and these associations become increasingly unreliable as we move farther from the training distribution.

These limitations collectively motivated researchers to develop more sophisticated positional encoding schemes, from Shaw's direct relative encodings to Transformer-XL's decomposed approach, ALiBi's distance-based penalties, and RoPE's elegant rotational solution, each addressing different aspects of these fundamental challenges.

You can find the discussion about the original positional encoding here:

Additive Relative Positional Embeddings

One of the first works addressing capturing the relative position between tokens instead of the absolute ones was done by Shaw et al in 2018. It addressed many of the original positional encoding's shortcomings. Instead of having an embedding matrix added to the semantic representation of the tokens, it modifies directly the computation of the attention layers with two positional embeddings. The first one a_ij^K is added to the key representation, and the second a_ij^V, to the value representation:

\(\begin{align} \mathbf{k}_j \rightarrow \mathbf{k}_j + \mathbf{a}_{ij}^K \nonumber\\ \mathbf{v}_j \rightarrow \mathbf{v}_j + \mathbf{a}_{ij}^V \end{align}\)

where a_ij^K and a_ij^V are learned embeddings of size d_model that depend only on the relative distance j-i. Those embeddings are learned in each attention layer and influence more directly the interactions between tokens. Ignoring the attention heads for simplicity, the computation of a context vector c_i is modified as:

\( \mathbf{c}_i = \sum_{j=1}^N \text{Softmax}\left(\frac{\mathbf{q}_i^T\left(\mathbf{k}_j+\mathbf{a}_{ij}^K\right)}{\sqrt{d_\text{model}}}\right)\left(\mathbf{v}_j+\mathbf{a}_{ij}^V\right)\)

They clip the maximum relative distance to a constant L, learning only 2L+1 position embeddings for each positional encoding. If we call the matrices of learned positions w^K and w^V, the actual relative position representations that are added to keys and values are the clipped version of those matrices:

\(\begin{align} \mathbf{a}_{ij}^K = w^K_{\text{clip}(j-i, L)} \nonumber\\ \mathbf{a}_{ij}^V = w^V_{\text{clip}(j-i, L)} \end{align}\)

where

\(\text{clip}(j-i, L)=\max\left(-L, \min\left(L, j-i\right)\right)\)

which clamps the relative distance to the range [−L, L]. This means that for any relative distance j-i > L,

\(\mathbf{a}_{ij}^K = \mathbf{a}_{i,i+L}^K\)

and any relative distance j-i < -L,

\(\mathbf{a}_{ij}^K = \mathbf{a}_{i,i-L}^K\)

In practice, L can be chosen quite small as the performance remained relatively stable for L > 2 (testing L = 4, L = 16, L = 64, and L = 256). This suggests that distinguishing the precise relative distances of tokens becomes less important beyond a few positions away. The model primarily needs fine-grained position information for nearby contexts, while more distant relationships can be effectively captured with less positional precision, allowing the content representations themselves to drive attention patterns at longer distances. Even with a very small clipping window (L = 2), the model with relative positional encoding achieved substantial improvements over absolute positioning.

Despite the added performance gain, it is important to note that it is at the cost of added parameters and added time complexity. At the time, Shaw et al. performed their experiments with a 65M parameters transformer model with 6 layers and d_model = 512. We need two new parameter layers of size (2L+1) x d_model, and with L = 16, it is ~200K additional parameters, which is negligible compared to the overall size of the model. More importantly, computing all the relative distances between the N tokens, the constant memory access, and adding the related embeddings is an O(N²) process that imposes a significant additional computational work on top of the already quadratic complexity of attention.

Multiplicative Relative Positional Embeddings

In a previous newsletter, we introduced the attention mechanism developed with Transformer-XL to handle arbitrarily long sequences, but we left out the discussion about the positional encoding. Developing a new relative positional encoding was one of the critical pieces to handle longer sequences. The approach is based on the following analysis we provided in a previous newsletter for the original positional encoding:

\(\begin{align} e_{i,i+k}\sqrt{d_\text{model}} &= \quad\underbrace{\mathbf{x}_i^\top W^{Q\top} W^K \mathbf{x}_{i+k}}_{\text{Token-Token Interaction}} \nonumber\\ &+\quad \underbrace{\mathbf{x}_i^\top W^{Q\top} W^K \mathbf{PE}(i) R(k)}_{\text{Token-Position Interaction}} \nonumber\\ &+ \quad\underbrace{\mathbf{PE}(i)^\top W^{Q\top} W^K \mathbf{x}_{i+k}}_{\text{Position-Token Interaction}}\nonumber\\ &+\quad \underbrace{\mathbf{PE}(i)^\top W^{Q\top} W^K \mathbf{PE}(i) R(k)}_{{\text{Position-Position Interaction}}} \end{align}\)

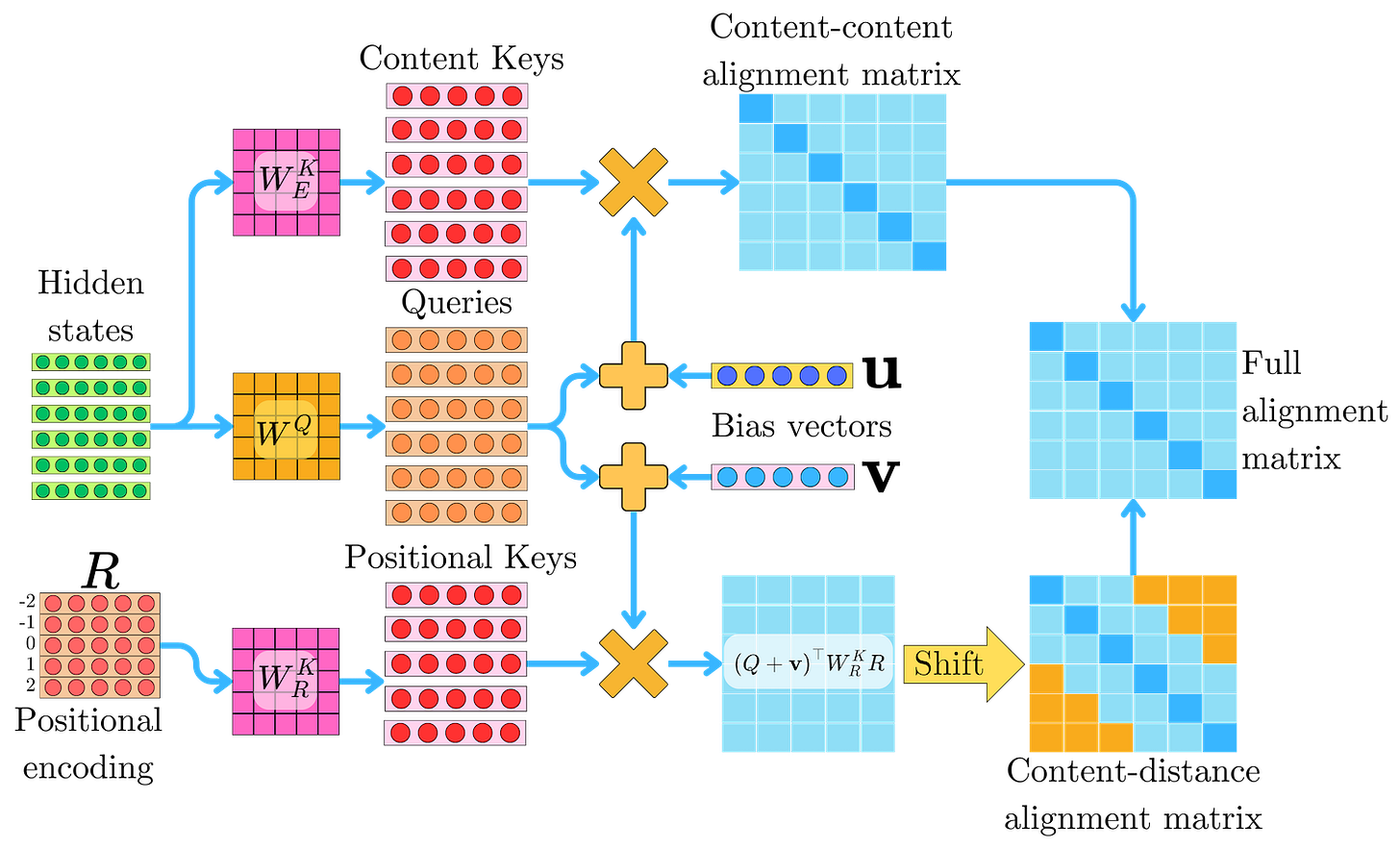
In this equation, we decomposed the contributions from the different content and positional components for the first attention layer in the model when using the vanilla absolute positional encoding. We showed how R(k) was capturing the relative positional information between tokens, and we hope for the model to learn W^Q and W^K such that it can effectively utilize that information. To help the model capture better the content and position interactions between tokens, the relative positional encoding introduced in Transformer-XL modified this original equation. The relative positional encoding will now be applied within every layer following this strategy:

• x_i^T W^QT W^K x_i+k originally captured the pure content-based interaction between tokens. x_i, in the original Transformer, represents the embedding vector from the token embedding, and the related hidden state h_i is the sum of the token embedding and the positional encoding:

  \( \mathbf{h}_{i} = \mathbf{x}_{i} + \mathbf{PE}(i)\)

  We modify this interaction by applying it directly to the hidden states h_i and h_i+k where k is the distance between the related tokens:

  \( \mathbf{h}_i^\top W^{Q\top} W^K_E \mathbf{h}_{i+k}\)

  We specifically distinguish the projection W_E^K to be content-specific.

• x_i^T W^QT W^K PE(i) R(k) or equivalently x_i^T W^QT W^K PE(i+k) R(k) captured a token's preference for attending to positions was tied to fixed locations. However, this is confusing for the model because PE(i+k) depends on the specific position of x_i. Instead, in the Transformer-XL, they modified this interaction only accounting for the relative distance k from the hidden state h_i:

  \(\mathbf{h}_i^\top W^{Q\top} W^K_R \mathbf{r}_k\)

  r_k is a vector of the positional encoding matrix R. As for the additive relative positional embeddings, R is a (2L+1) x d_model matrix where r_k only depends on the relative distance between h_i and h_i+k, and L is a constant chosen to clip the maximum distances that can be represented. However, R is not a learned parameter matrix, but a fixed encoding as in the original Transformer architecture. W_R^K (different from W_E^K) is a specialized weight matrix that further enhances this separation of positional processing.

• PE(i)^T W^QT W^K x_i+k is a position-dependent bias for attending to content. This is a strange term because it has more or less weight depending on the position of the query. To make it position independent, we replace PE(i)^T W^QT with a global learnable parameter u^T:

  \(\mathbf{u}^\top W^K_E \mathbf{h}_{i+k}\)

  u is a vector of size d_model. This reflects an insight that the attentive bias toward different content should remain consistent regardless of the query position. In other words, the importance of certain word types doesn't need to depend on position, so a single global parameter can replace position-specific queries. This simplifies the model while maintaining expressiveness.

• PE(i)^T W^QT W^K PE(i+k) is a position-position iteration term that depends on the specific position of the query. To make it position independent while keeping the relative positional information, we introduce another global learnable parameter v^T of size d_model to replace PE(i)^T W^QT, and use again the relative positional encoding R:

  \( \mathbf{v}^\top W^K_R \mathbf{r}_k\)

  As before, we use the position-specific projection W_R^K. The intuition is that certain relative distances might be generally more important than others, regardless of the absolute positions involved. For example, adjacent tokens (small k) might generally be more related than distant ones, regardless of their absolute positions in the sequence.

This leads to redefining the alignment scores as:

\(\begin{align} e_{i,i+k}\sqrt{d_\text{model}} &= \quad\underbrace{\mathbf{h}_i^\top W^{Q\top} W^K_E \mathbf{h}_{i+k}}_{\text{Token-Token Interaction}} \nonumber\\ &+\quad \underbrace{\mathbf{h}_i^\top W^{Q\top} W^K_R \mathbf{r}_k}_{\text{Token-Position Interaction}} \nonumber\\ &+ \quad\underbrace{\mathbf{u}^\top W^K_E \mathbf{h}_{i+k}}_{\text{Position-Token Interaction}}\nonumber\\ &+\quad \underbrace{\mathbf{v}^\top W^K_R \mathbf{r}_k}_{\text{Position-Position Interaction}} \end{align}\)

with W^Qh_i = q_i, the query and W_E^Kh_i+k = k_i+k, the key, we can regroup the terms:

\( e_{i,i+k}\sqrt{d_\text{model}} = \left(\mathbf{q}_i+\mathbf{u}\right)^\top\mathbf{k}_{i+k}+\left(\mathbf{q}_i+\mathbf{v}\right)^\top W_R^K\mathbf{r}_{k}\)

with

\(\left(\mathbf{q}_i+\mathbf{u}\right)^\top\mathbf{k}_{i+k}\)

being a pure content interaction term and

\(\left(\mathbf{q}_i+\mathbf{v}\right)^\top W_R^K\mathbf{r}_{k}\)

representing a content-to-relative distance interaction term. W_E^Kh_i+k = k_i+k can be thought of as a content contribution to the key, while W_R^Kr_k is the relative positional piece of the key. The global parameters u and v can be seen as providing "default query projections" that are active regardless of the specific query token. This ensures that important content and positional patterns always receive some attention.

R follows the same sinusoidal encoding function as the original Transformer, just applied to relative positions instead of absolute positions:

\(\text{R}(k, j) = \begin{cases} \sin\left(\frac{k}{10000^{j/d_\text{model}}}\right) & \text{if $j$ is even} ,\\ \cos\left(\frac{k}{10000^{(j-1)/d_\text{model}}}\right) & \text{if $j$ is odd}, \end{cases}\)

where k is the relative distance between positions, ranging from −L to +L, and j is the dimension index from 0 to d_model.

Computing

\(\left(\mathbf{q}_i+\mathbf{v}\right)^\top W_R^K\mathbf{r}_{k}\)

requires careful thought to limit the complexity of the problem. With N tokens, we could naively extract all the N² related r_k since there are N² pairs of tokens. However, there would be many duplicate vectors since different pairs of tokens have the same distance between them. Instead, we can directly use the whole R matrix and pass it through the linear layer W_R^K:

\(K_R=W_R^KR\)

R is a (2L+1) x d_model, and W_R^K is a d_model x d_model matrix, therefore the "positional keys" K_R is a (2L+1) x d_model matrix. As a consequence

\(\left(\mathbf{q}_i+\mathbf{v}\right)^\top W_R^K\mathbf{r}_{k}\)

is a (2L+1) dimensional vector which leads to a (2L+1) x N content to position alignment matrix for N queries.

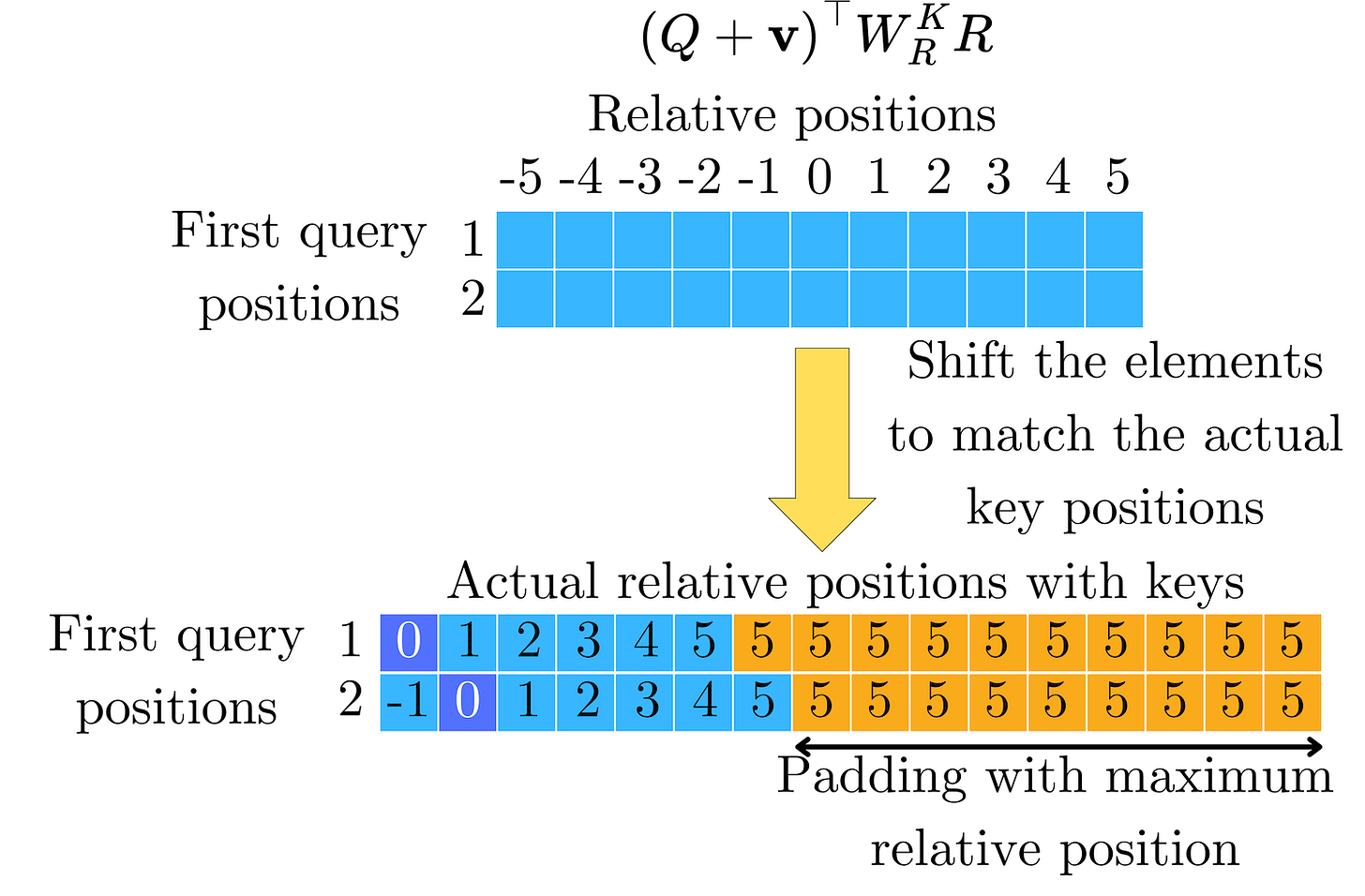
Let's make sure we understand the different tensors in play. We have the queries Q = [q₁, …, q_N], the keys K = [k₁, …, k_N], and the positional equivalent to the keys K_R =[W_R^Kr_-L, …, W_R^Kr_L]. The relative positions in K_R are not aligned with the relative positions of K with respect to Q. This means we cannot simply add

\((Q + \mathbf{u})^\top K \quad\text{with}\quad (Q + \mathbf{v})^\top K_R\)

because of the misalignment in the key ordering. We just need to change the indices of the elements in (Q + v)^T K_R. For query position i, we need:

• For key position 0: a relative distance i−0 = i

• For key position 1: a relative distance i−1

• For key position 2: a relative distance i−2

• And so on...

In other words, for the i-th row of the content to position alignment matrix P = (Q + v)^T K_R, we need to select values in a specific pattern. The solution is to reshape and shift the P matrix so that the correct relative position scores align with the positions we need in the final attention matrix.

In the case of Transformer-XL, remember that the sequences are processed in segments of size n « N, and the attention mechanism per segment follows an O(n²) time complexity. W_R^KR also operates on segments, and the time complexity is

\(\mathcal{O}\left((2L+1)nd_\text{model}\right)=\mathcal{O}\left(Lnd_\text{model}\right)\)

The shift operation needs at least O(n²) operations to reindex the alignment score matrix. Therefore, the overall time complexity associated with the relative positional encoding follows the asymptotic behavior O(n²).

Transformer-XL showed improvements in the model's ability to utilize longer contexts. When trained with segments of length 128 but evaluated with various attention lengths, the model showed continued improvements in perplexity up to 640 tokens. The paper reported improved perplexity metric when increasing evaluation context length beyond training length, something absolute encoding couldn't achieve.

ALiBi: Attention With Linear Biases

The relative positional encoding developed in Transformer-XL is designed to handle very long sequences, but it adds complexity to the attention layer, and, while it can handle longer contexts through its recurrence mechanism, it was not specifically designed for extrapolation to arbitrary lengths beyond training. ALiBi (Attention With Linear Biases) was introduced in 2021 as a simpler approach that could easily be extrapolated to much longer sequences than the ones seen during training. It does not require any model parameters and can be expressed as a penalty on the alignment score:

\(e_{ij} = \mathbf{q}_i^\top \mathbf{k}_j + m_h\left(j-i\right)\)

where j-i is the distance between the query q_i and the key k_j, and m_h is a head-specific constant, with h being the index of the head. In the case of causal language modeling, we always have j-i ≤ 0, leading to lower attention for far-away tokens. ALiBi tends to sacrifice true long-range modeling for extrapolation capability. m_h is chosen as:

\(m_h=2^{-\frac{8h}{n_\text{head}}}\)

where h ∈ [0, …, n_head -1]. For example, if we have 8 heads, the first head would have m₀ = 2⁰ = 1, and the last head m₇ = 2^-7 = 0.0078125, with a spectrum of the different intermediary slopes in between. For j-i = 1000, for example, we get m₇(j-i)~ -7.8, which is a substantial penalty to capture long-range interaction between tokens. This suggests that ALiBi may not be optimal for tasks requiring very long-range dependencies (like book-length coherence), but it represents a valuable engineering trade-off that improves efficiency without sacrificing performance on many practical tasks.

Despite this limitation, ALiBi works well for extrapolation for several reasons:

• Graduated attention ranges: The different head slopes create a spectrum of attention distances. While no head truly specializes in very long-range attention, the collection of heads creates a gradient of focus distances.

• Local coherence dominance: Language has a hierarchical structure where local coherence (within paragraphs or nearby sentences) often matters more than very distant relationships. The bias aligns with this natural property of language.

• Information propagation: Information can still flow across long distances through multiple layers of the transformer. Even if direct attention across 1000 tokens is penalized, information can propagate through intermediate positions across layers.

• Relative vs. absolute positioning: Unlike sinusoidal embeddings that break down completely outside their training range, ALiBi's linear bias at least provides a consistent, predictable signal at any distance.

The paper showed that a model trained on 512 tokens could handle sequences of 3072 tokens with better perplexity than a sinusoidal model trained on 3072 tokens. A 1.3 billion parameter model trained on 1024 tokens achieved the same perplexity as a sinusoidal model trained on 2048 tokens when evaluated on 2048-token sequences. As input length increases beyond training length, sinusoidal models' performance degrades almost immediately while ALiBi's performance continues improving up to ~2-3x training length before plateauing.

RoPE: Rotary Position Embedding

The Rotary Position Embedding (RoPE) is now one of the most common strategies used to inject the relative positional information within the attention mechanism. The idea behind RoPE is to rotate the keys and queries based on the position of the related tokens in the input sequences. This will inject the absolute positional information directly into the queries and keys. Let's look at a toy example to understand the logic. Let's consider a 2-dimensional query q_i and a 2-dimensional key k_j. To rotate 2-dimensional vectors, we use rotation matrices: