How LLMs Generate Text

• The Greedy Search Generation

• The Multinomial Sampling Generation

• The Beam Search Generation

• The Contrastive Search Generation

• Generating Text with the Transformers package by Hugging Face

---

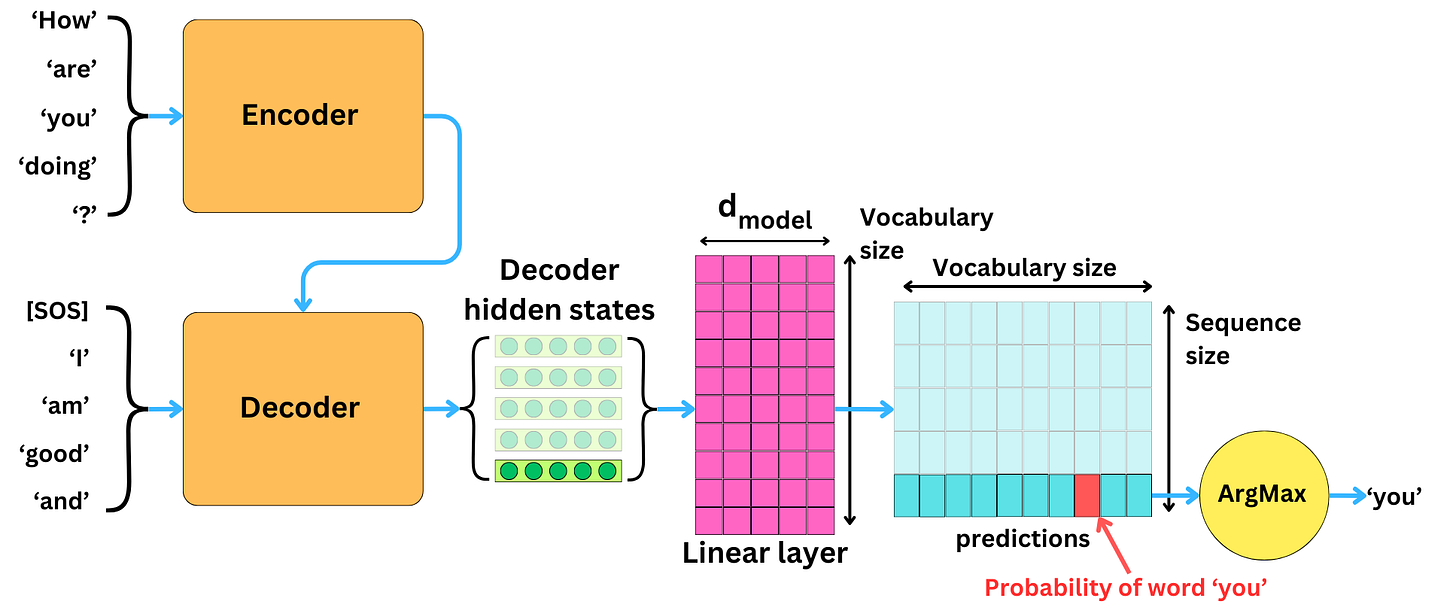
The Greedy Search Generation

Earlier, we saw how we applied the ArgMax function to the probability vector to generate the predictions. This is a greedy approach.

We just take the word that corresponds to the highest probability.

The greedy search generation has a few advantages:

• Speed and Simplicity

• Deterministic Output

• Good for Short Sequences

• Resource Efficiency

And it has a few problems:

• Lack of Diversity

• Local Optima

• Poor Long-Term Coherence

• Risk of Degeneration

• Suboptimal for Complex Tasks

• Inflexibility

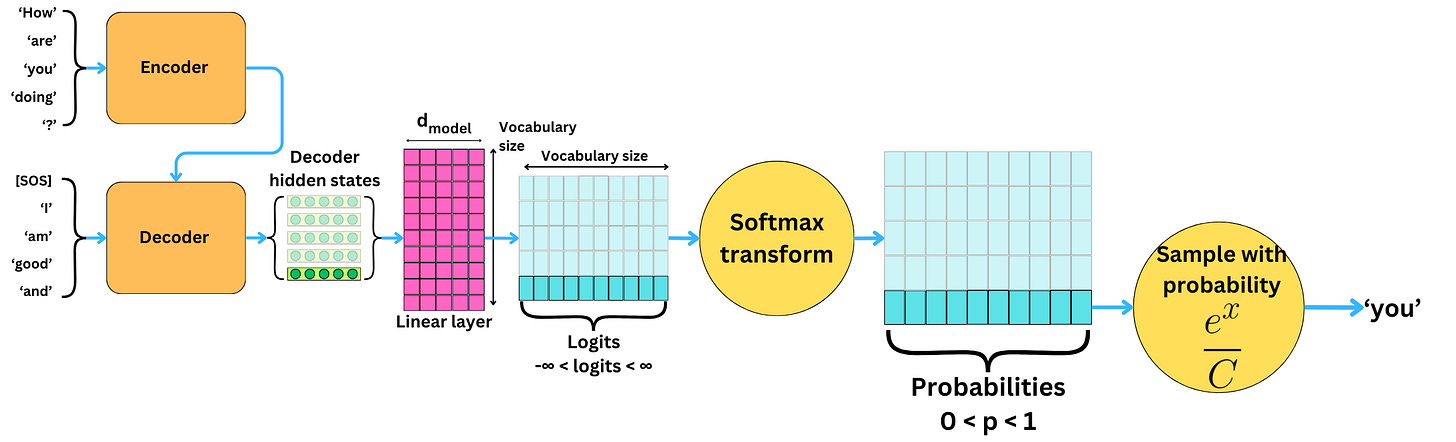
The Multinomial Sampling Generation

Earlier, we actually ignored the fact that to obtain probabilities, we need to take the Softmax transformation.

The Softmax transformation ensures that the values are bounded within [0, 1]. It also accentuates the largest value while reducing the other values. That is why it is called the “soft maximum“ function.

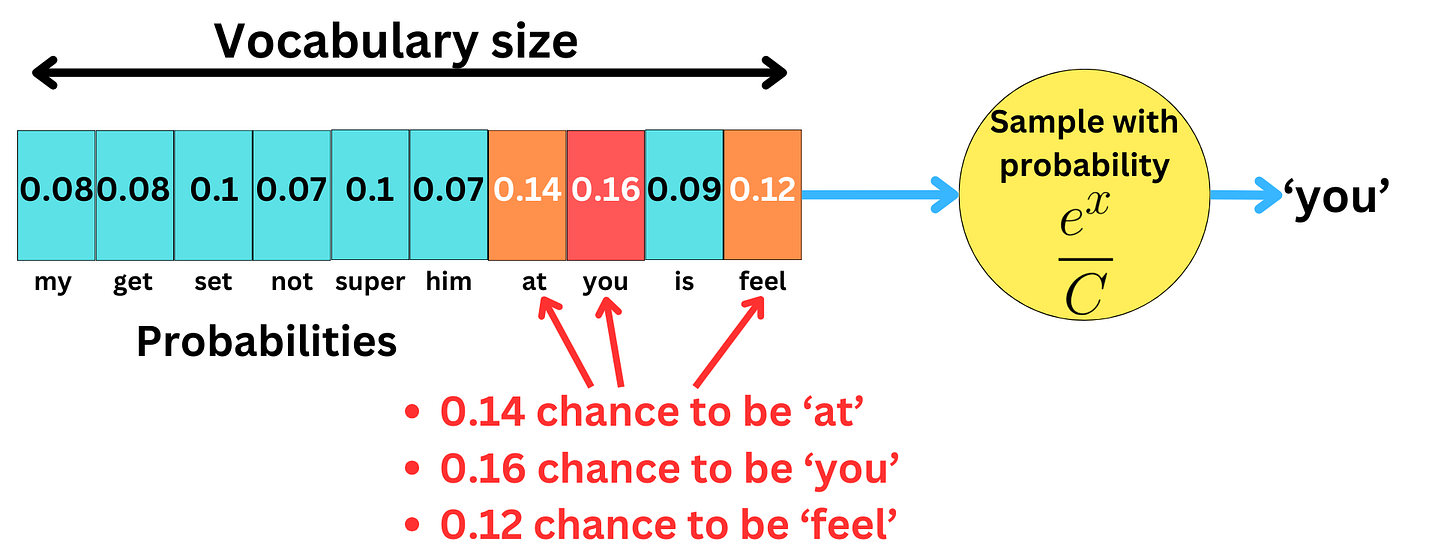
Having probabilities allows us to sample the words based on the predicted probabilities.

If we sample based on probabilities, different words may be selected at each iteration.

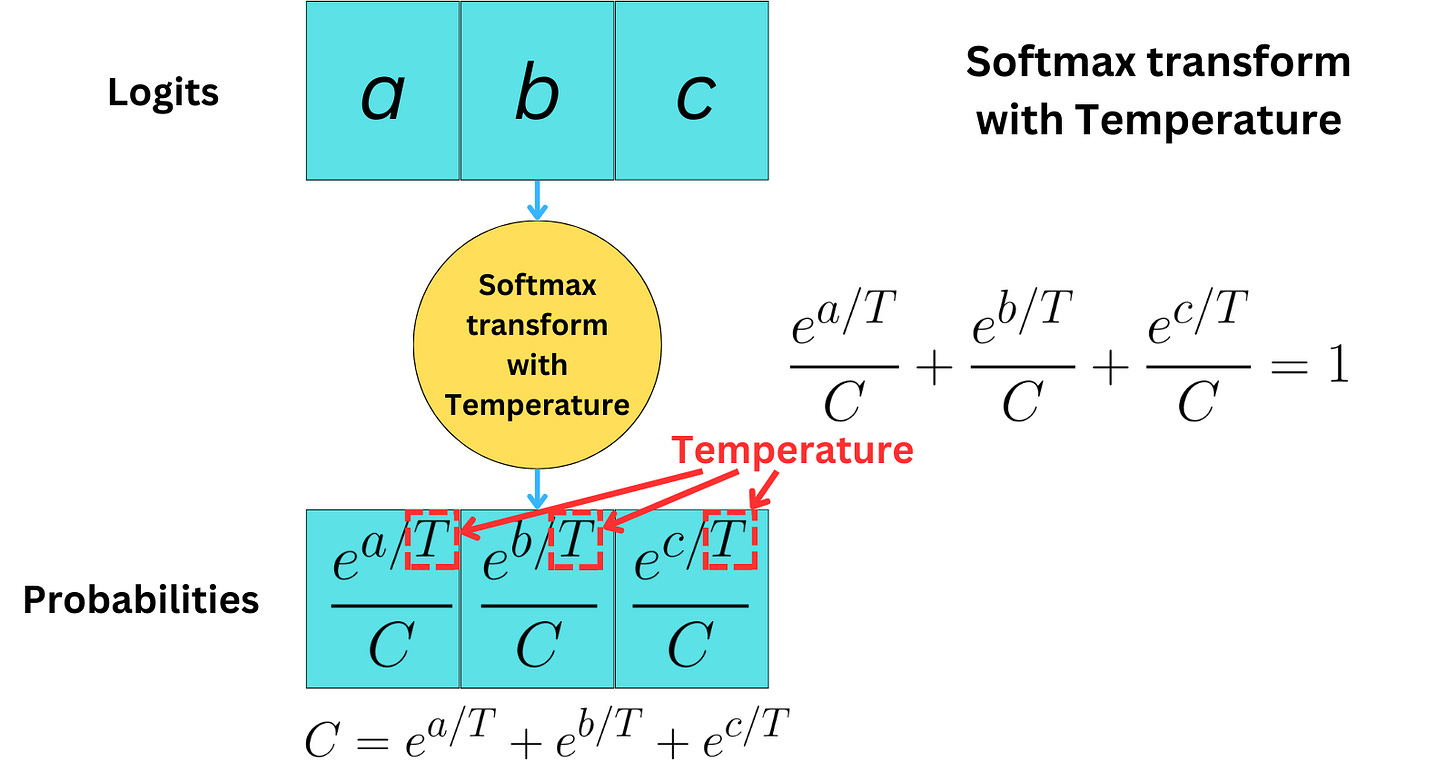
The problem with the Softmax transformation is that we are very dependent on the specific analytical form of that function. To induce more flexibility, we can introduce the temperature parameter.

Low temperature will induce a behavior close to the greedy approach, whereas high temperature will lead to uniformly random sampling.

The term “temperature“ is used because this Softmax function is known in physics as the Boltzmann or Gibbs distribution. It provides the distribution of the energy levels of a group of particles.

The multinomial distribution has a few advantages:

• Diversity and Creativity

• Reduced Repetitiveness

• Better Exploration of the Model's Capabilities

• Useful for Certain Applications

But also a few problems:

• Reduced Coherence

• Unpredictability

• Quality Control

• Difficulty in Controlling Output

• Dependency on Temperature Setting

• Less Suitable for Certain Tasks

The Beam Search Generation

In the case of the greedy search and the multinomial sampling, we iteratively look for the next best token conditioned on the prompt and the previous tokens.

But those are not the probabilities we care about. We care about generating the best sequence of tokens conditioned on a specific prompt.

Fortunately we can compute the probability we care about from the probabilities predicted by the model.

That is important because there could exist a sequence of tokens with a higher probability than the one generated by the greedy search.

Finding the best sequence is an NP-hard problem, but we can simplify the problem by using a heuristic approach. At each step of the decoding process, we assess multiple candidates, and we use the beam width hyperparameter to keep the top best sequences.

We iterate this process for the N tokens we need to decode, and we keep only the sequence with the highest probability.

Beam search has a few advantages:

• Balance Between Quality and Efficiency

• Flexibility through Beam Width

• Good for Long Sequences

• Useful in Structured Prediction Tasks

• Can be combined with Multinomial sampling

And a few problems:

• Suboptimal Solutions

• Computational Cost

• Length Bias

• Lack of Diversity

• Heuristic Nature

• End-of-Sequence Prediction

The Contrastive Search Generation

The contrastive search generation method aims to penalize undesired behavior like lack of diversity.

At each step, we choose the highest probability tokens, and we penalize them with a similarity metric computed with the previously generated tokens. In the first iteration, there are no previous tokens.

In the second iteration, we have only one token to penalize.

In the third iteration, we have multiple previous tokens, so we use the max function to penalize with the highest similarity value.

And we iterated this process.

Contrastive search has a few advantages:

• Improved Diversity and Quality

• Reduced Repetitiveness

• Better Contextual Relevance

• Customizable

And a few disadvantages:

• Computational Complexity

• Dependency on Scoring Function

• Potential for Reduced Fluency

• Difficulty in Balancing Criteria

• Heuristic Nature

• Scalability Issues

Generating Text with the Transformers package by Hugging Face

Let’s test how we can generate text with the transformers package. Let’s get the model:

from transformers import AutoModelForCausalLM, AutoTokenizer

model_id = "gpt2"
tokenizer = AutoTokenizer.from_pretrained(model_id)
model = AutoModelForCausalLM.from_pretrained(
    model_id, 
    pad_token_id=tokenizer.eos_token_id
)

And we write a function to generate text:

def generate(text, kwargs={}):
    inputs = tokenizer(text, return_tensors="pt")
    output = model.generate(max_length=512, **inputs, **kwargs)
    result = tokenizer.decode(output[0], skip_special_tokens=True)
    return result

The following will lead to a greedy search:

text = "How are you?"

config = {
    'num_beams': 1,
    'do_sample': False,
}
  
result = generate(text, config)

The following will lead to multinomial sampling with temperature:

text = "How are you?"

config = {
    'num_beams': 1,
    'do_sample': True,
    'temperature': 0.7
}
  
result = generate(text, config)

The following will lead to a beam search:

text = "How are you?"

config = {
    'num_beams': 5,
    'do_sample': False,
}
  
result = generate(text, config)

The following will lead to a beam search with multinomial sampling:

text = "How are you?"

config = {
    'num_beams': 5,
    'do_sample': True,
}
  
result = generate(text, config)

The following will lead to a contrastive search:

text = "How are you?"

config = {
    'penalty_alpha': 1.,
    'top_k': 6,
}
  
result = generate(text, config)